Designing a Simple Machine
Prior to the use of modern currency, payments were made by trading goods. Those goods could sometimes be paid for with precious metals: copper, silver, or gold. The copper, silver, and gold coins were literally "worth their weight," so a method had to be devised to determine the weight of the metal offered in copper, silver, and gold compared to the good being purchased. Merchants maintained scales or balances for this purpose.
A balance is a simple mechanical device that illustrates many fundamental principles and can be easily built and assembled. By designing a balance according to the following steps, you will be doing the following:
-
Utilizing the density and specific gravity of solid and liquid materials to perform a force balance
-
Utilizing the principles of geometry and algebra to calculate the weight and force acting on the balance beam
-
Reading engineering drawings to relate numerical values to real parts and components of the balance.
Two drawings show a PVC pipe and endcap that will be used to hold water in the balance. A third drawing shows a wooden balance beam.
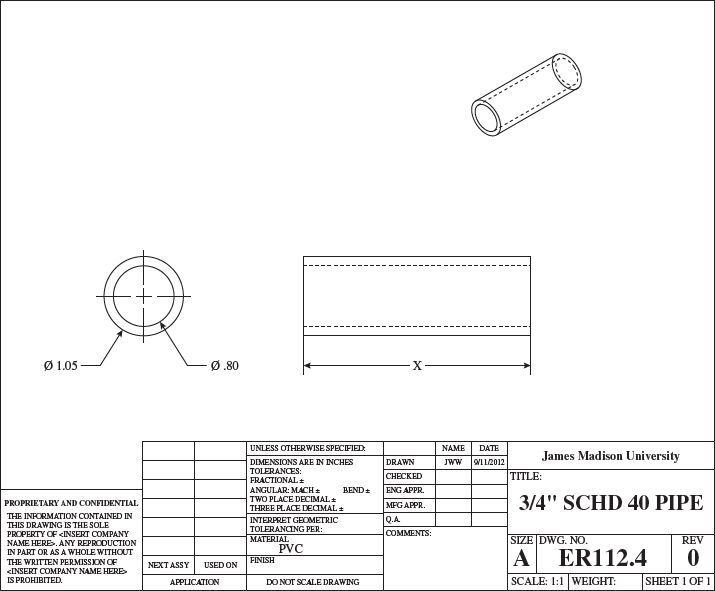
A diagram of a 3⁄4″ SCHD 40 pipe is shown. The pipe is represented as a hollow cylinder of length x, outer diameter 1.05 inches, and inner diameter 0.80 inches. Both ends of the pipe are open. Drawn by JWW during date 9/11/2012 for James Madison University. Scale is 1:1 with Size A.
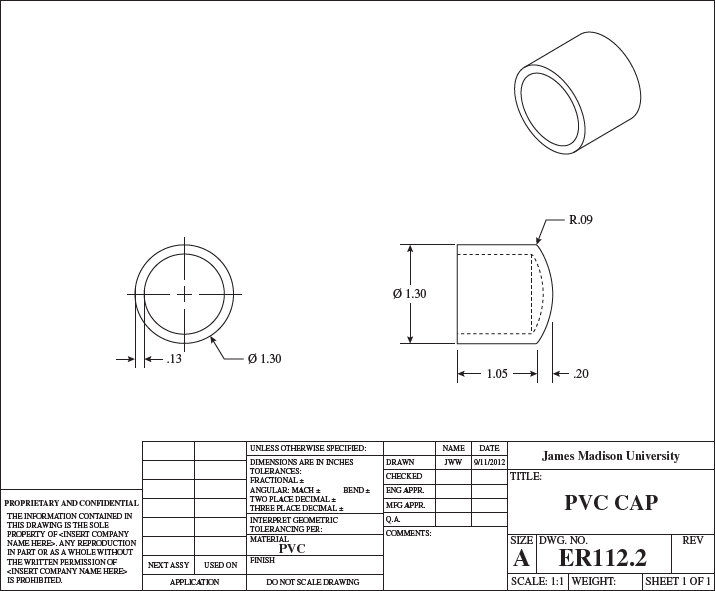
A diagram of a PVC cap is shown. The cap is represented as a hollow cylinder of length 1.05 inches, outer diameter 1.30 inches, and thickness 0.13 inches, with the left end of the cap open and the right end of the cap closed. The closed end is represented as a dome with its peak along the axis of the cylinder, base flush against the cylinder, with width of base equal to the outer diameter of cylinder, and height of 0.20 inches from base to peak. The cap is labeled R.09. Drawn by JWW during date 9/11/2012 for James Madison University. Scale is 1:1 with Size A.
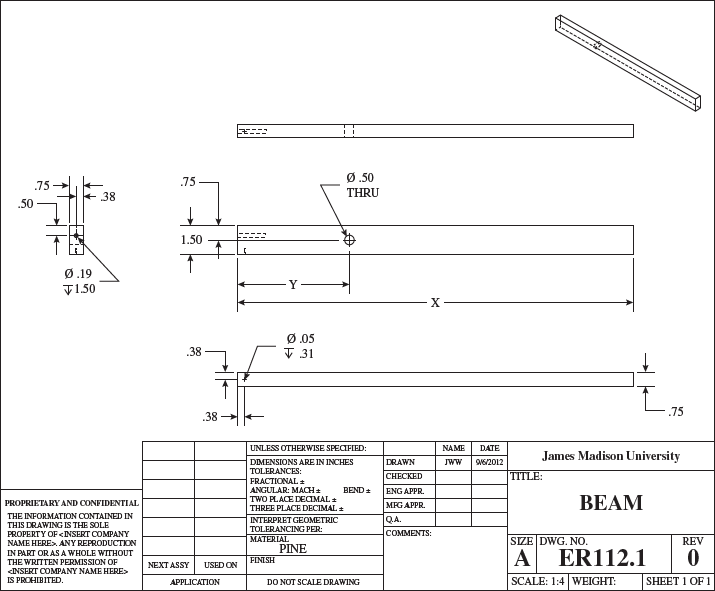
An engineering drawing shows five views of a wooden beam with several holes drilled into it. All dimensions are in inches.
-
The first view of the beam, at the left of the diagram, is a vertical rectangle showing the cross section of the beam. The cross section has a height of 1.50 and a width of 0.75. The distance from the beam's center to the right side is approximately 0.38.
- The first hole is drilled from left to right completely through the cross section.
- The second hole is drilled into the page, has a diameter of 0.19, and is drilled to a depth of 1.50.
Both the top of the first hole and the center of the second hole are a distance of 0.50 from the top side of the cross section.
-
The second view is a view of the beam from the top. Hidden lines show the first hole drilled completely through the beam from one long face upward to the other, perpendicular to the normal to the cross section. The second hole is drilled from the left side a short distance to the right, coaxial with the normal to the cross section.
- The third view is a side view of the beam. The beam has length X. The first hole has a diameter of 0.50 and is drilled into the page, fully through the beam. Its center is a distance Y < X⁄2 from the left end of the beam and a height of 0.75 from either the top or bottom side. The second hole is drilled from the left side a short distance to the right.
-
The fourth view is a view of the beam from the bottom. The width is 0.75. A third hole of diameter 0.05 is drilled into one end at a distance of 0.38 from the top side, 0.38 from the end, and to a depth of 0.31.
-
The fifth view is an isometric view of the beam.
At the bottom of the drawing, the following information is given.
-
A box at the lower left corner reads PROPRIETARY AND CONFIDENTIAL. THE INFORMATION CONTAINED IN THIS DRAWING IS THE SOLE PROPERTY OF [INSERT COMPANY NAME HERE]. ANY REPRODUCTION IN PART OR AS A WHOLE WITHOUT THE WRITTEN PERMISSION OF [INSERT COMPANY NAME HERE] IS PROHIBITED.
-
To the right of this box, there is a table entitled Application with two columns, headed NEXT ASSY and USED ON. The table has six empty rows.
-
To the right of the table, there is a column of six boxes containing the following text, from top to bottom:
-
UNLESS OTHERWISE SPECIFIED:
-
DIMENSIONS ARE IN INCHES
TOLERANCES:
FRACTIONAL ±
ANGULAR: MACH ± BEND ±
TWO PLACE DECIMAL ±
THREE PLACE DECIMAL ±
-
INTERPRET GEOMETRIC TOLERANCING PER:
-
MATERIAL PINE
-
FINISH
-
DO NOT SCALE DRAWING
-
To the right of this column, a two-column, five-row table has column headers NAME and DATE and row headers DRAWN, CHECKED, ENG APPR., MFG APPR., AND Q.A. The entries in the DRAWN row are JWW and 9/11/2012. The other four rows are empty. There is a box labeled COMMENTS: below the table.
-
To the right of this table, at the lower right corner of the diagram, eight boxes read as follows:
-
James Madison University
-
Title: BEAM
-
Size: A
-
DWG. NO. ER112.1
-
REV 0
-
SCALE: 1:4
-
WEIGHT:
-
SHEET 1 OF 1
In some of the steps below, you will be asked to submit a sentence, paragraph, or file. Your submission will be graded by your instructor after the due date based on its accuracy. Your grade may change.
-
Calculate the following, given that water has a density of approximately 1,000 kg/m3 and PVC has a density of approximately 1,380 kg/m3. (Enter masses in grams.)
Considering the precision that we will be able to attain in building the balance, is it acceptable to disregard the dome-shaped end of the cap and assume a flat shape for your calculations? Why or why not?
-
-
The aluminum bar will be held on a nail at one end. The PVC tube containing water will be suspended from a nail at the other end of the beam.
Once you have determined the masses of the PVC assembly, the wooden beam, and the aluminum counterbalance in previous steps, sketch the beam and illustrate the point where the beam is attached to a vertical frame. Also, show the forces and the direction of the forces acting on the beam from the aluminum counterbalance on the right-hand side of the beam and the water-filled PVC tube on the left-hand side of the beam. (Submit a file with a maximum size of 15 MB.)
-
-
Using tools provided to you, construct a balance and place it on a pin on a stand or one available in the classroom. Is your beam perfectly balanced (i.e., does it hang from the pin in a perfectly level and horizontal position)? Describe possible sources of error in the construction of the beam that might cause the beam to be less than perfectly balanced.
-
In the days before common currency, merchants may have developed poor reputations if people felt they were being cheated. Would it be relatively simple or difficult to change the way a scale behaved if a merchant were trying to balance coppers (copper coins) and receive an adjusted weight in silver? Describe how a dishonest merchant might "tip the scales."