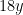WebAssign is not supported for this browser version. Some features or content might not work. System requirements

WebAssign

Welcome, demo@demo

(sign out)

Saturday, March 29, 2025 00:39 EDT

Home My Assignments Grades Communication Calendar My eBooks

Larson and Edwards - Calculus ET 8/e (Homework)

James Finch

Math - College, section 1, Fall 2019

Instructor: Dr. Friendly

Current Score : 17 / 37

Due : Sunday, January 27, 2030 00:00 EST

Last Saved : n/a Saving...  ()

Ask Your Teacher Print Assignment
Question
Points
1 2 3 4 5 6 7 8 9 10
2/2 1/1 7/7 6/6 0/6 1/4 –/7 –/2 –/1 0/1
Total
17/37 (45.9%)

  • Instructions

    WebAssign provides a wide range of exercises that enable you to:

    • Build problem-solving skills (#1-3: Read Its, Watch Its, and (optional) Master Its)
    • Develop Conceptual Understanding (#4-7: Master It Tutorials, How Do You See It? Exercises, Explore Its, Proof Problems, and Expanded Problems)
    • Address Readiness Gaps (#8-10: Just in Time, QuickPrep, and Calculus Readiness Bootcamp Exercises)

    This demo assignment allows many submissions and allows you to try another version of the same question for practice wherever the problem has randomized values.

    The answer key and solutions will display after the first submission for demonstration purposes. Instructors can configure these to display after the due date or after a specified number of submissions.

Assignment Submission

For this assignment, you submit answers by question parts. The number of submissions remaining for each question part only changes if you submit or change the answer.

Assignment Scoring

Your last submission is used for your score.

1. 2/2 points  |  Previous Answers LarCalcET8 2.4.049. My Notes
Question Part
Points
Submissions Used
1 2
1/1 1/1
4/50 1/50
Total
2/2
 
  • This exercise will build problem-solving skills.
  • Read It links are available as a learning tool under each question so students can quickly jump to the corresponding section of the eTextbook.
  • Students get just-in-time learning support with Watch It videos that contain narrated and closed-captioned videos walking students through the proper steps to solve a similar problem.

Find the x-values (if any) at which f is not continuous. If there are any discontinuities, determine whether they are removable. (Enter your answers as comma-separated lists. If an answer does not exist, enter DNE.)
f(x) = 
3
4 − x2
removable discontinuities x=
DNE
Correct: Your answer is correct. nonremovable discontinuities x=
2, −2
Correct: Your answer is correct.

Need Help? Watch It

Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
2. 1/1 points  |  Previous Answers LarCalcET8 2.3.087.MI. My Notes
Question Part
Points
Submissions Used
1
1/1
2/50
Total
1/1
 
  • This exercise will build problem-solving skills.
  • Master It tutorials are an optional student-help tool available within select questions for just-in-time support. Students can use the tutorial to guide them through the problem-solving process step-by-step using different numbers.

Consider the following function.
f(x) = 8x2 − 9x
Find the limit.
lim Δx→0 
f(x + Δx) − f(x)
Δx
16x−9
Correct: Your answer is correct.

Need Help? Master It

Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
3. 7/7 points  |  Previous Answers LarCalcET8 3.5.010.MI.SA. My Notes
Question Part
Points
Submissions Used
1 2 3 4 5 6 7
1/1 1/1 1/1 1/1 1/1 1/1 1/1
1/50 1/50 2/50 2/50 1/50 1/50 1/50
Total
7/7
 
  • This exercise will build problem-solving skills.
  • Master It tutorials are an optional student-help tool available within select questions for just-in-time support. Students can use the tutorial to guide them through the problem-solving process step-by-step using different numbers.

This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part.

Tutorial Exercise
Find dy/dx by implicit differentiation.
8x2y + 9y2x = −6
Step 1
To find the implicit derivative of the given function, we first take the derivative of both sides with respect to x. This means for any term involving only the variable x, we take the derivative as normal. For any term involving y, as y is a function of x, taking the derivative of y with respect to x is like using the Chain Rule. We note that the derivative of y is not 1, but
dy
dx
.
The given implicit function is
8x2y + 9y2x = −6.
 We can begin by taking the derivative of the right side of this equation with respect to x.
d
dx
[−6] =
$$0
Correct: Your answer is correct. webMathematica generated answer key
Step 2
By the additive property of the derivative, to find the derivative of the left-hand side of
8x2y + 9y2x = −6.
 we can find the derivative of each term separately.
The first term of the left side of the equation is
8x2y.
 Use the product rule to find the derivative of this term with respect to x.
d
dx
[8x2y]		 = 8x2 
dy
dx
 + y 
d
dx
[8x2]
 = 8x2 
dy
dx
 + y 
$$16x
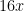
Correct: Your answer is correct. webMathematica generated answer key
The second term of the left side of the equation is
9y2x.
 Use the product rule again to find the derivative of this term with respect to x.
d
dx
[9y2x]		 = 9y2 
d
dx
[x] + x 
d
dx
[9y2]
 = 9y2(1) + x 
$$18y
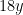
Correct: Your answer is correct. webMathematica generated answer key
 
dy
dx
Therefore, by the additive property of the derivative, the derivative of the left side of the equation is as follows.
d
dx
[8x2y] + 
d
dx
[9y2x] = 8x2 
dy
dx
 + y(16x) + 9y2(1) + x 
$$18y
Correct: Your answer is correct. webMathematica generated answer key
dy
dx
Step 3
We have found the derivative of each side of the implicit function
8x2y + 9y2x = −6.
 as follows.
d
dx
[8x2y] + 
d
dx
[9y2x]		 = 8x2 
dy
dx
 + 16xy + 9y2 + 18xy 
dy
dx
 
d
dx
[−6]		 = 0
Setting these derivatives equal to each other gives the derivative of the implicit function.
8x2 
dy
dx
 + 16xy + 9y2 + 18xy 
dy
dx
 = 0
Next, we solve for
dy
dx
.
 First, collect all terms involving
dy
dx
 on the left side of the equation.
8x2 
dy
dx
 + 16xy + 9y2 + 18xy 
dy
dx
 = 0
8x2 
dy
dx
 + 18xy 
dy
dx
 = 
$$−9y2−16xy
Correct: Your answer is correct. webMathematica generated answer key
Step 4
Finally, to solve for
dy
dx
,
 factor out
dy
dx
 on the left-hand side and divide both sides by the resulting factor.
8x2 
dy
dx
 + 18xy 
dy
dx
 = −16xy − 9y2
 
dy
dx
$$8x2+18xy
Correct: Your answer is correct. webMathematica generated answer key
 = −16xy − 9y2
 
dy
dx
 = 
$$(−16xy−9y2)8x2+18xy​
Correct: Your answer is correct. webMathematica generated answer key
You have now completed the Master It.
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
4. 6/6 points  |  Previous Answers LarCalcET8 5.4.062. My Notes
Question Part
Points
Submissions Used
1 2 3 4 5 6
1/1 1/1 1/1 1/1 1/1 1/1
1/50 1/50 1/50 1/50 1/50 1/50
Total
6/6
 
  • This exercise will develop conceptual understanding.
  • How Do You See It? exercises present a problem that students solve through visual inspection -- using the concepts learned in the lesson they've just completed.

The graph of a function f is shown in the figure.
The x y-coordinate plane is given. There is a curve and two shaded regions on the graph.
  • The curve f begins at the origin, goes down and right becoming less steep, changes direction in the fourth quadrant, goes up and right becoming more steep, passes through the x−axis at x = 2, goes up and right becoming less steep, changes direction in the first quadrant, goes down and right becoming more steep, and ends on the x−axis at x = 6.
  • The first region is labeled A and is below the x−axis and above the curve between x = 0 and x = 2.
  • The second region is labeled B and is above the x−axis and below the curve between x = 2 and x = 6.
The shaded region A has an area of 3.5, and
6
0
f(x) dx = 8.5.
 Use this information to fill in the blanks. (Round your answer for part (f) to four decimal places.)
(a)
2
0
f(x) dx = Correct: Your answer is correct.
(b)
6
2
f(x) dx = Correct: Your answer is correct.
(c)
6
0
|f(x)| dx = Correct: Your answer is correct.
(d)
2
0
−2f(x) dx = Correct: Your answer is correct.
(e)
6
0
[2 + f(x)] dx = Correct: Your answer is correct.
(f)
The average value of f over the interval [0, 6] is Correct: Your answer is correct. .
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
5. 0/6 points  |  Previous Answers LarCalcET8 7.1.EI.001. My Notes
Question Part
Points
Submissions Used
1 2 3 4 5 6
0/1 0/1 0/1 0/1 0/1 0/1
1/50 1/50 1/50 1/50 1/50 1/50
Total
0/6
 
  • This exercise will develop conceptual understanding.
  • Explore It exercises engage students with interactive learning modules that include video and explorations. The module is also available to use for studying in the eTextbook

Review the Explore It, then use it to complete the exercise below.
Click here to access the Explore It in a new window.
Select Function 1 under the Explore & Test section of the Explore It.
When integrating with respect to the x-axis, the formula for the approximate area, using n rectangles of equal width and left end points is:
Area ≈ 
n
i = 1
(
xi − 1
 − x2i − 1) Δx.
(a)
Set the number of rectangles in the simulation to 5. What is the approximate area? (Round your answer to five decimal places.)
Incorrect: Your answer is incorrect.
(b)
Set the number of rectangles in the simulation to 10. What is the approximate area? (Round your answer to five decimal places.)
Incorrect: Your answer is incorrect.
(c)
What is the formula, in terms of n, for the width Δx of each rectangle? Before submitting your answer, verify your answer with various numbers of rectangles in the simulation.
Δx =
2
Incorrect: Your answer is incorrect.
(d)
What is the formula, in terms of i and n, for the general left end point,
xi − 1?
 Before submitting your answer, verify your answer with various numbers of rectangles in the simulation.
xi − 1 =
2
Incorrect: Your answer is incorrect.
(e)
Using your answers to parts (c) and (d), give the general formula in terms of i and n for the approximate area when integrating with respect to the x-axis using n rectangles of equal width and left end points.
Area ≈ 
n
i = 1
2
Incorrect: Your answer is incorrect.
(f)
Set the number of rectangles to 2. As you increase the number of rectangles to 5, 10, 20, and 40, which rectangles give the better approximation, vertical rectangles (integration with respect to the x-axis) or horizontal rectangles (integration with respect to the y-axis)?
     Incorrect: Your answer is incorrect.
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
6. 1/4 points  |  Previous Answers LarCalcET8 2.5.082. My Notes
Question Part
Points
Submissions Used
1 2 3 4
1/1 0/1 0/1 0/1
1/50 2/50 2/50 2/50
Total
1/4
 
  • This exercise will develop conceptual understanding.
  • Automatically Graded Proof Problems develop an understanding of the entire process of writing proofs as students get practice and immediate feedback.

Use the
ε−δ
 definition of infinite limits to prove the statement.
lim x→5− 
1
x − 5
 = −∞
f(x) = 
1
x − 5
 is defined for all
x ≠ Correct: Your answer is correct. .
 Let
N < 0
 be given. Find
δ > 0
 such that
f(x) = 
1
x − 5
 < N
 whenever
5 − δ < x < 5.
 Let
δ = Incorrect: Your answer is incorrect. .
 Then for
|5 − δ| < x and x < 5, 
1
|x − 5|
 > 
1
δ
 = Incorrect: Your answer is incorrect. ,
 and
1
x − 5
 = − 
1
|x − 5|
 < Incorrect: Your answer is incorrect. .
 Thus
lim x→5− 
1
x − 5
 = −∞.
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
7. –/7 points LarCalcET8 4.1.029.EP. My Notes
Question Part
Points
Submissions Used
1 2 3 4 5 6 7
–/1 –/1 –/1 –/1 –/1 –/1 –/1
0/50 0/50 0/50 0/50 0/50 0/50 0/50
Total
–/7
 
  • This exercise will develop conceptual understanding.
  • Expanded Problems enhance student understanding by going beyond a basic exercise and asking students to solve each step of the problem in addition to their final answer.

Consider the following function and closed interval.
f(x) = x3 − 
3
2
x2,    [−5, 4]
Find
f '(x).
f '(x) =
Find the critical numbers of f in
(−5, 4)
 and evaluate f at each critical number. (Order your answers from smallest to largest x, then from smallest to largest y.)
(x, y)
=
(x, y)
=
Evaluate f at each endpoint of
[−5, 4].
left endpoint
(x, y)
=
right endpoint
(x, y)
=
Find the absolute extrema of the function on the closed interval
[−5, 4].
minimum
(x, y)
=
maximum
(x, y)
=
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
8. –/2 points LarCalcET8 3.7.JIT.009. My Notes
Question Part
Points
Submissions Used
1 2
–/1 –/1
0/50 0/50
Total
–/2
 
  • This exercise will address readiness gaps.
  • Just In Time exercises provide timely support by reviewing prerequisites within the context of new concepts throughout the course.

Express x and y in terms of trigonometric ratios of θ.
A right triangle is given.
  • The first side of length x is opposite an unlabeled angle.
  • The second side of length y is opposite the angle θ.
  • The third side of length 24 is opposite the right angle.
x =
y =

Need Help? Watch It

Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
9. –/1 points LarCalcET8 QP.12.003. My Notes
Question Part
Points
Submissions Used
1
–/1
0/50
Total
–/1
 
  • This exercise will address readiness gaps.
  • Quick Prep exercises address readiness gaps by reviewing prerequisite concepts and skills. They can be used early in the course or whenever needed.

Two polynomials P and D are given. Use either synthetic or long division to divide
P(x)
 by
D(x)
 and express the quotient
P(x)
D(x)
 in the form
P(x)
D(x)
 = Q(x) + 
R(x)
D(x)
.
P(x) = x2 + 4x − 8,    D(x) = x + 3
P(x)
D(x)
 =
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
10. 0/1 points  |  Previous Answers CalculusTP1 2.3.010. My Notes
Question Part
Points
Submissions Used
1
0/1
1/50
Total
0/1
 
  • This exercise will address readiness gaps.
  • The Calculus Readiness Bootcamp contains a formative student assessment on prerequisite topics needed for success and targeted learning modules for areas where students struggled.

Evaluate
(f ∘ g)(−3).
f(x) = x + 6;    g(x) = 4x2 − 8
3434
Incorrect: Your answer is incorrect.
Recall that (f ∘ g)(x) = f(g(x)). Is the given numerical value for x substituted in g or in f? Then, where is that resulting value substituted?
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
Home My Assignments
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter an exact number.