Larson & Edwards - Calculus (AP Edition) 12/e (Homework)

James Finch

Math - High School, section 1, Fall 2019

Instructor: Dr. Friendly

Current Score : 9 / 39

Due : Monday, January 28, 2030 12:00 EST

Last Saved : n/a Saving... ()

Print Assignment

Question

Points

1	2	3	4	5	6	7	8	9	10	11	12
0/1	1/1	2/2	1/1	–/7	4/6	0/6	1/4	–/7	–/2	–/1	–/1

Total

9/39 (23.1%)

Instructions
WebAssign provides a wide range of exercises that enable you to:
- Prepare for the AP^® Calculus Exam (#1–2: AP^® Practice Questions and FT5 Test Preparation Guide)
- Build problem-solving skills (#3–5: Watch Its and (optional) Master Its)
- Develop Conceptual Understanding (#6–9: Master It Tutorials, How Do You See It? Exercises, Explore Its, Proof Problems, Read Its, and Expanded Problems)
- Address Readiness Gaps (#10–12: Just in Time, QuickPrep, and Calculus Readiness Bootcamp Exercises)
Please read the information in the box at the top of each exercise to learn more about the features, content, and/or grading. We encourage you to try correct and incorrect answers in any answer blanks.

Assignment Submission

For this assignment, you submit answers by question parts. The number of submissions remaining for each question part only changes if you submit or change the answer.

Assignment Scoring

Your last submission is used for your score.

1. 0/1 points | Previous Answers LarCalc12HS 2.AP.008. My Notes

This exercise will help students prepare for the AP^® Calculus Exam.
Each chapter of single-variable calculus has a set of multiple-choice AP^® Practice Questions that gives students examples of the types of question they will see on the exam.

The table shows the position

s(t)

of a particle that moves along a straight line at several times t, where t is measured in seconds and s is measured in meters.

t	2.0	2.7	3.2	3.8
s(t)	5.2	7.8	10.6	12.2

Which of the following best estimates the velocity of the particle at

t = 3?

(A) 3.7 m/sec (B) 3.9 m/sec (C) 5.6 m/sec (D) 7.8 m/sec

Viewing Saved Work Revert to Last Response

2. 1/1 points | Previous Answers LarCalc12HS FT5.1.004. My Notes

This exercise will help students prepare for the AP^® Calculus Exam.
This is a sample multiple-choice question from the Fast Track to a Five (FT5) AP^® test preparation guide. This guide includes strategies for taking the exam, a diagnostic test so that students can assess their level of preparedness, chapter-review sections with self-study questions in AP^® format, and two complete practice tests in AP^® format.

Evaluate the limit, if it exists.

lim x→1

tan⁻¹(x)

sin⁻¹(x) + 1

(A)

(B)

(C)

(D)

2π + 4

Solution or Explanation

(D). Evaluate the limit numerically (direct substitution).

lim x→1

tan⁻¹(x)

sin⁻¹(x) + 1

+ 1

π + 2

2π + 4

Viewing Saved Work Revert to Last Response

3. 2/2 points | Previous Answers LarCalc12HS 1.4.047. My Notes

This exercise will build problem-solving skills.
Students get just-in-time learning support with Watch It videos that contain narrated and closed-captioned videos walking students through the proper steps to solve a similar problem.

Find the x-values (if any) at which f is not continuous. If there are any discontinuities, determine whether they are removable. (Enter your answers as comma-separated lists. If an answer does not exist, enter DNE.)

f(x) =

4 − x²

removable discontinuities x=

DNE

$webMathematica generated answer key$ nonremovable discontinuities x=

−2,2

$webMathematica generated answer key$

Solution or Explanation

f(x) =

4 − x²

(2 − x)(2 + x)

has nonremovable discontinuities at

x = ± 2

because

lim x → 2 f(x)

and

lim x → −2 f(x)

do not exist.

Need Help?

Viewing Saved Work Revert to Last Response

4. 1/1 points | Previous Answers LarCalc12HS 1.3.085.MI. My Notes

This exercise will build problem-solving skills.
Master It tutorials are an optional student-help tool available within select questions for just-in-time support. Students can use the tutorial to guide them through the problem-solving process step-by-step using different numbers.

Consider the following function.

f(x) = 8x² − 5x

Find the limit.

lim Δx→0

f(x + Δx) − f(x)

Δx

16x−5

$webMathematica generated answer key$

Solution or Explanation

lim

Δx → 0

f(x + Δx) − f(x)

Δx

lim

Δx → 0

8(x + Δx)² − 5(x + Δx) − (8x² − 5x)

Δx

lim

Δx → 0

8x² + 16xΔx + 8Δx² − 5x − 5Δx − 8x² + 5x

Δx

lim

Δx → 0

Δx(16x + 8Δx − 5)

Δx

lim

Δx → 0

(16x + 8Δx − 5)

16x − 5

Need Help?

Viewing Saved Work Revert to Last Response

5. –/7 points LarCalc12HS 2.5.010.MI.SA. My Notes

This exercise will build problem-solving skills.
Master It tutorials—Standalone are embedded, step-by-step tutorials used to help students understand each step required to solve the problem, before inputting their final answer.

This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part.

Find dy/dx by implicit differentiation.

2x²y + 7y²x = −6

Viewing Saved Work Revert to Last Response

6. 4/6 points | Previous Answers LarCalc12HS 4.4.062. My Notes

This exercise will develop conceptual understanding.
How Do You See It? exercises present a problem that students solve through visual inspection—using the concepts learned in the lesson they've just completed.

The graph of a function f is shown in the figure.

The x y-coordinate plane is given. There is a curve and two shaded regions on the graph.
The curve f begins at the origin, goes down and right becoming less steep, changes direction in the fourth quadrant, goes up and right becoming more steep, passes through the x−axis at x = 2, goes up and right becoming less steep, changes direction in the first quadrant, goes down and right becoming more steep, and ends on the x−axis at x = 6.
The first region is labeled A and is below the x−axis and above the curve between x = 0 and x = 2.
The second region is labeled B and is above the x−axis and below the curve between x = 2 and x = 6.

The shaded region A has an area of 7.5, and

f(x) dx = 15.5.

Use this information to fill in the blanks. (Round your answer for part (f) to four decimal places.)

(a)

f(x) dx =

-7.5

(b)

f(x) dx =

23.0

(c)

|f(x)| dx =

30.5

(d)

−2f(x) dx =

15.0

(e)

[2 + f(x)] dx =

27.5

(f)

The average value of f over the interval [0, 6] is

2.5833

Solution or Explanation

(a)

Because

y < 0

on [0, 2],

f(x) dx = −(area of region A) = −7.5.

(b)

f(x) dx = (area of region B) =

f(x) dx −

f(x) dx = 15.5 − (−7.5) = 23.0

(c)

|f(x)| dx = −

f(x) dx +

f(x) dx = 7.5 + 23.0 = 30.5

(d)

−2f(x) dx = −2

f(x) dx = −2(−7.5) = 15.0

(e)

[2 + f(x)] dx =

2 dx +

f(x) dx = 12 + 15.5 = 27.5

(f)

average value =

f(x) dx =

(15.5) = 2.5833

Viewing Saved Work Revert to Last Response

7. 0/6 points | Previous Answers LarCalc12HS 7.1.EI.001. My Notes

This exercise will develop conceptual understanding.
Explore It exercises engage students with interactive learning modules that include video and explorations. The module is also available to use for studying in the eTextbook

Review the Explore It, then use it to complete the exercise below.

Click here to access the Explore It in a new window.

Select Function 1 under the Explore & Test section of the Explore It.

When integrating with respect to the x-axis, the formula for the approximate area, using n rectangles of equal width and left end points is

Area ≈

n

i = 1

(

x_{i − 1}

− x²_{i − 1}) Δx.

(a)

Set the number of rectangles in the simulation to 5. What is the approximate area? (Round your answer to five decimal places.)

0.30974

(b)

Set the number of rectangles in the simulation to 10. What is the approximate area? (Round your answer to five decimal places.)

0.32551

(c)

What is the formula, in terms of n, for the width Δx of each rectangle? Before submitting your answer, verify your answer with various numbers of rectangles in the simulation.

Δx =

$webMathematica generated answer key$

(d)

What is the formula, in terms of i and n, for the general left end point, x_{i − 1}? Before submitting your answer, verify your answer with various numbers of rectangles in the simulation.

x_{i − 1} =

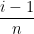
$webMathematica generated answer key$

(e)

Using your answers to parts (c) and (d), give the general formula in terms of i and n for the approximate area when integrating with respect to the x-axis using n rectangles of equal width and left end points.

Area ≈

n

i = 1

$webMathematica generated answer key$

(f)

Set the number of rectangles to 2. As you increase the number of rectangles to 5, 10, 20, and 40, which rectangles give the better approximation, vertical rectangles (integration with respect to the x-axis) or horizontal rectangles (integration with respect to the y-axis)?

vertical rectangles horizontal rectangles sometimes vertical and sometimes horizontal They give the same approximation.

Viewing Saved Work Revert to Last Response

8. 1/4 points | Previous Answers LarCalc12HS 1.5.082. My Notes

This exercise will develop conceptual understanding.
Automatically graded Proof Problems develop an understanding of the entire process of writing proofs as students get practice and immediate feedback.
Read It links are available as a learning tool under each question so students can quickly jump to the corresponding section of the eTextbook.

Use the

ε−δ

definition of infinite limits to prove the statement.

lim x→5⁻

x − 5

= −∞

f(x) =

x − 5

is defined for all

x ≠

Let

N < 0

be given. Find

δ > 0

such that

f(x) =

x − 5

< N

whenever

5 − δ < x < 5.

Let

δ =

−1/𝘕

Then for

|5 − δ| < x and x < 5,

|x − 5|

−𝘕

and

x − 5

= −

|x − 5|

𝘕

Thus

lim x→5⁻

x − 5

= −∞.

Viewing Saved Work Revert to Last Response

9. –/7 points LarCalc12HS 3.1.027.EP. My Notes

This exercise will develop conceptual understanding.
Expanded Problems go beyond a basic exercise to ask students to show the specific steps of their work or to explain the reasoning behind the answers they've provided.

Consider the following function and closed interval.

f(x) = x³ −

x², [−1, 4]

Find

f '(x).

f '(x) =

Find the critical numbers of f in

(−1, 4)

and evaluate f at each critical number. (Order your answers from smallest to largest x, then from smallest to largest y.)

(x, y)

Evaluate f at each endpoint of

[−1, 4].

left endpoint

(x, y)

right endpoint

(x, y)

Find the absolute extrema of the function on the closed interval

[−1, 4].

minimum

(x, y)

maximum

(x, y)

Viewing Saved Work Revert to Last Response

10. –/2 points LarCalc12HS 2.6.JIT.009. My Notes

This exercise will address readiness gaps.
Just In Time exercises provide timely support by reviewing prerequisites within the context of new concepts throughout the course.

Express x and y in terms of trigonometric ratios of θ.

A right triangle is given.
The first side of length x is opposite an unlabeled angle.
The second side of length y is opposite the angle θ.
The third side of length 20 is opposite the right angle.

x =

y =

Need Help?

Viewing Saved Work Revert to Last Response

11. –/1 points LarCalc12HS QP.12.003. My Notes

This exercise will address readiness gaps.
Quick Prep exercises address readiness gaps by reviewing prerequisite concepts and skills. They can be used early in the course or whenever needed.

Two polynomials P and D are given. Use either synthetic or long division to divide

P(x)

D(x)

and express the quotient

P(x)

D(x)

in the form

P(x)

D(x)

= Q(x) +

R(x)

D(x)

P(x) = x² + 6x − 12, D(x) = x + 5

P(x)

D(x)

Viewing Saved Work Revert to Last Response

12. –/1 points calculustp1 2.3.010.defective My Notes

This exercise will address readiness gaps.
The Calculus Readiness Bootcamp contains a formative student assessment on prerequisite topics needed for success and targeted learning modules for areas where students struggled.

Evaluate

(f ∘ g)(−2).

f(x) = x + 9; g(x) = 8x² − 2

Viewing Saved Work Revert to Last Response

1	2
1/1	1/1
1/100	1/100

WebAssign

Welcome, demo@demo

Larson & Edwards - Calculus (AP Edition) 12/e (Homework)

Current Score : 9 / 39

Due : Monday, January 28, 2030 12:00 EST

Last Saved : n/a Saving... ()

Instructions

Assignment Submission

Assignment Scoring