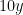WebAssign is not supported for this browser version. Some features or content might not work. System requirements

WebAssign

Welcome, demo@demo

(sign out)

Saturday, March 29, 2025 02:46 EDT

Home My Assignments Grades Communication Calendar My eBooks

Larson & Edwards - Calculus 12/e (Homework)

James Finch

Math - College, section 1, Fall 2019

Instructor: Dr. Friendly

Current Score : 29 / 37

Due : Sunday, January 27, 2030 00:00 EST

Last Saved : n/a Saving...  ()

Ask Your Teacher Print Assignment
Question
Points
1 2 3 4 5 6 7 8 9 10
2/2 0/1 7/7 6/6 3/6 4/4 3/7 2/2 1/1 1/1
Total
29/37 (78.4%)

  • Instructions

    WebAssign provides a wide range of exercises that enable you to:
    • Build problem-solving skills (#1–3: Watch Its and (optional) Master Its)
    • Develop Conceptual Understanding (#4–7: Master It Tutorials, How Do You See It? Exercises, Explore Its, Proof Problems, Read Its, and Expanded Problems)
    • Address Readiness Gaps (#8–10: Just in Time, QuickPrep, and Calculus Readiness Bootcamp Exercises)
    Please read the information in the box at the top of each exercise to learn more about the features, content, and/or grading. We encourage you to try correct and incorrect answers in any answer blanks.

Assignment Submission

For this assignment, you submit answers by question parts. The number of submissions remaining for each question part only changes if you submit or change the answer.

Assignment Scoring

Your last submission is used for your score.

1. 2/2 points  |  Previous Answers LarCalc12 1.4.047. My Notes
Question Part
Points
Submissions Used
1 2
1/1 1/1
7/100 1/100
Total
2/2
 
  • This exercise will build problem-solving skills.
  • Students get just-in-time learning support with Watch It videos that contain narrated and closed-captioned videos walking students through the proper steps to solve a similar problem.
Find the x-values (if any) at which f is not continuous. If there are any discontinuities, determine whether they are removable. (Enter your answers as comma-separated lists. If an answer does not exist, enter DNE.)
f(x) = 
5
4 − x2
removable discontinuities x=
DNE
Correct: Your answer is correct. webMathematica generated answer key nonremovable discontinuities x=
−2,2
Correct: Your answer is correct. webMathematica generated answer key


Solution or Explanation
f(x) = 
5
4 − x2
 = 
5
(2 − x)(2 + x)
 has nonremovable discontinuities at
x = ± 2
 because
lim x → 2 f(x)
 and
lim x → −2 f(x)
 do not exist.

Need Help? Watch It

Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
2. 0/1 points  |  Previous Answers LarCalc12 1.3.085.MI. My Notes
Question Part
Points
Submissions Used
1
0/1
3/100
Total
0/1
 
  • This exercise will build problem-solving skills.
  • Master It tutorials are an optional student-help tool available within select questions for just-in-time support. Students can use the tutorial to guide them through the problem-solving process step-by-step using different numbers.
Find
lim Δx→0 
f(x + Δx) − f(x)
Δx
.
f(x) = 4x2 − 3x
−3
Incorrect: Your answer is incorrect. webMathematica generated answer key


Solution or Explanation
lim
Δx → 0
 
f(x + Δx) − f(x)
Δx
 = 
lim
Δx → 0
 
4(x + Δx)2 − 3(x + Δx) − (4x2 − 3x)
Δx
 
 = 
lim
Δx → 0
 
4x2 + 8xΔx + 4Δx2 − 3x − 3Δx − 4x2 + 3x
Δx
 
 = 
lim
Δx → 0
 
Δx(8x + 4Δx − 3)
Δx
 = 
lim
Δx → 0
 (8x + 4Δx − 3)
 = 8x − 3

Need Help? Master It

Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
3. 7/7 points  |  Previous Answers LarCalc12 2.5.010.MI.SA. My Notes
Question Part
Points
Submissions Used
1 2 3 4 5 6 7
1/1 1/1 1/1 1/1 1/1 1/1 1/1
2/100 1/100 1/100 2/100 3/100 1/100 1/100
Total
7/7
 
  • This exercise will build problem-solving skills.
  • Master It tutorials—Standalone are embedded, step-by-step tutorials used to help students understand each step required to solve the problem, before inputting their final answer.

This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part.

Tutorial Exercise
Find dy/dx by implicit differentiation.
2x2y + 5y2x = −2
Step 1
To find the implicit derivative of the given function, we first take the derivative of both sides with respect to x. This means for any term involving only the variable x, we take the derivative as normal. For any term involving y, as y is a function of x, taking the derivative of y with respect to x is like using the Chain Rule. We note that the derivative of y is not 1, but
dy
dx
.
The given implicit function is
2x2y + 5y2x = −2.
 We can begin by taking the derivative of the right side of this equation with respect to x.
d
dx
[−2] =
$$0
Correct: Your answer is correct. webMathematica generated answer key
Step 2
By the additive property of the derivative, to find the derivative of the left-hand side of
2x2y + 5y2x = −2.
 we can find the derivative of each term separately.
The first term of the left side of the equation is
2x2y.
 Use the product rule to find the derivative of this term with respect to x.
d
dx
[2x2y]		 = 2x2 
dy
dx
 + y 
d
dx
[2x2]
 = 2x2 
dy
dx
 + y 
$$4x
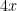
Correct: Your answer is correct. webMathematica generated answer key
The second term of the left side of the equation is
5y2x.
 Use the product rule again to find the derivative of this term with respect to x.
d
dx
[5y2x]		 = 5y2 
d
dx
[x] + x 
d
dx
[5y2]
 = 5y2(1) + x 
$$10y
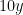
Correct: Your answer is correct. webMathematica generated answer key
 
dy
dx
Therefore, by the additive property of the derivative, the derivative of the left side of the equation is as follows.
d
dx
[2x2y] + 
d
dx
[5y2x] = 2x2 
dy
dx
 + y(4x) + 5y2(1) + x 
$$10y
Correct: Your answer is correct. webMathematica generated answer key
dy
dx
Step 3
We have found the derivative of each side of the implicit function
2x2y + 5y2x = −2.
 as follows.
d
dx
[2x2y] + 
d
dx
[5y2x]		 = 2x2 
dy
dx
 + 4xy + 5y2 + 10xy 
dy
dx
 
d
dx
[−2]		 = 0
Setting these derivatives equal to each other gives the derivative of the implicit function.
2x2 
dy
dx
 + 4xy + 5y2 + 10xy 
dy
dx
 = 0
Next, we solve for
dy
dx
.
 First, collect all terms involving
dy
dx
 on the left side of the equation.
2x2 
dy
dx
 + 4xy + 5y2 + 10xy 
dy
dx
 = 0
2x2 
dy
dx
 + 10xy 
dy
dx
 = 
$$−4xy−5y2
Correct: Your answer is correct. webMathematica generated answer key
Step 4
Finally, to solve for
dy
dx
,
 factor out
dy
dx
 on the left-hand side and divide both sides by the resulting factor.
2x2 
dy
dx
 + 10xy 
dy
dx
 = −4xy − 5y2
 
dy
dx
$$2x2+10xy
Correct: Your answer is correct. webMathematica generated answer key
 = −4xy − 5y2
 
dy
dx
 = 
$$(−4xy−5y2)2x2+10xy​
Correct: Your answer is correct. webMathematica generated answer key
You have now completed the Master It.
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
4. 6/6 points  |  Previous Answers LarCalc12 4.4.062. My Notes
Question Part
Points
Submissions Used
1 2 3 4 5 6
1/1 1/1 1/1 1/1 1/1 1/1
4/100 1/100 1/100 1/100 1/100 3/100
Total
6/6
 
  • This exercise will develop conceptual understanding.
  • How Do You See It? exercises present a problem that students solve through visual inspection—using the concepts learned in the lesson they've just completed.
The graph of a function f is shown in the figure. The shaded region A has an area of 5.5, and
6
0
f(x) dx = 12.5.
 Use this information to fill in the blanks. (Round your answer for part (f) to four decimal places.)
The x y-coordinate plane is given. There is a curve and two shaded regions on the graph.
  • The curve begins at the origin, goes down and right becoming less steep, changes direction in the fourth quadrant, goes up and right becoming more steep, passes through the x-axis at x = 2, goes up and right becoming less steep, changes direction in the first quadrant, goes down and right becoming more steep, and ends on the x-axis at x = 6.
  • The first region is labeled A and is below the x-axis and above the curve between x = 0 and x = 2.
  • The second region is labeled B and is above the x-axis and below the curve between x = 2 and x = 6.
(a)
2 f(x) dx
0
 = Correct: Your answer is correct. seenKey

-5.5
(b)
6 f(x) dx
2
 = Correct: Your answer is correct. seenKey

18.0
(c)
6 |f(x)| dx
0
 = Correct: Your answer is correct. seenKey

23.5
(d)
2 −2f(x) dx
0
 = Correct: Your answer is correct. seenKey

11.0
(e)
6 [2 + f(x)] dx
0
 = Correct: Your answer is correct. seenKey

24.5
(f)
The average value of f over the interval [0, 6] is Correct: Your answer is correct. seenKey

2.0833

 .


Solution or Explanation
(a)
Because
y < 0
 on [0, 2],
2 f(x) dx
0
 = −(area of region A) = −5.5.
(b)
6 f(x) dx
2
 = (area of region B) = 
6 f(x) dx
0
 − 
2 f(x) dx
0
 = 12.5 − (−5.5) = 18.0
(c)
6 |f(x)| dx
0
 = −
2 f(x) dx
0
 + 
6 f(x) dx
2
 = 5.5 + 18.0 = 23.5
(d)
2 −2f(x) dx
0
 = −2
2 f(x) dx
0
 = −2(−5.5) = 11.0
(e)
6 [2 + f(x)] dx
0
 = 
6 2 dx
0
 + 
6 f(x) dx
0
 = 12 + 12.5 = 24.5
(f)
Average value = 
1
6
6 f(x) dx
0
 = 
1
6
(12.5) = 2.0833
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
5. 3/6 points  |  Previous Answers LarCalc12 7.1.EI.001. My Notes
Question Part
Points
Submissions Used
1 2 3 4 5 6
1/1 0/1 0/1 1/1 0/1 1/1
2/100 1/100 1/100 1/100 1/100 2/100
Total
3/6
 
  • This exercise will develop conceptual understanding.
  • Explore It exercises engage students with interactive learning modules that include video and explorations. The module is also available to use for studying in the eTextbook

Review the Explore It, then use it to complete the exercise below.
Click here to access the Explore It in a new window.
Select Function 1 under the Explore & Test section of the Explore It.
When integrating with respect to the x-axis, the formula for the approximate area, using n rectangles of equal width and left end points is
Area ≈ 
n
i = 1
(
xi − 1
 − x2i − 1) Δx.
(a)
Set the number of rectangles in the simulation to 5. What is the approximate area? (Round your answer to five decimal places.)
Correct: Your answer is correct. seenKey

0.30974
(b)
Set the number of rectangles in the simulation to 10. What is the approximate area? (Round your answer to five decimal places.)
Incorrect: Your answer is incorrect. seenKey

0.32551
(c)
What is the formula, in terms of n, for the width Δx of each rectangle? Before submitting your answer, verify your answer with various numbers of rectangles in the simulation.
Δx =
12
Incorrect: Your answer is incorrect. webMathematica generated answer key
(d)
What is the formula, in terms of i and n, for the general left end point, xi − 1? Before submitting your answer, verify your answer with various numbers of rectangles in the simulation.
xi − 1 =
(i−1)n​
Correct: Your answer is correct. webMathematica generated answer key
(e)
Using your answers to parts (c) and (d), give the general formula in terms of i and n for the approximate area when integrating with respect to the x-axis using n rectangles of equal width and left end points.
Area ≈ 
n
i = 1
−e3Δx
Incorrect: Your answer is incorrect. webMathematica generated answer key
(f)
Set the number of rectangles to 2. As you increase the number of rectangles to 5, 10, 20, and 40, which rectangles give the better approximation, vertical rectangles (integration with respect to the x-axis) or horizontal rectangles (integration with respect to the y-axis)?
     Correct: Your answer is correct.
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
6. 4/4 points  |  Previous Answers LarCalc12 1.5.082. My Notes
Question Part
Points
Submissions Used
1 2 3 4
1/1 1/1 1/1 1/1
1/100 2/100 2/100 2/100
Total
4/4
 
  • This exercise will develop conceptual understanding.
  • Automatically graded Proof Problems develop an understanding of the entire process of writing proofs as students get practice and immediate feedback.
  • Read It links are available as a learning tool under each question so students can quickly jump to the corresponding section of the eTextbook.
Use the
ε−δ
 definition of infinite limits to prove the statement.
lim x→5− 
1
x − 5
 = −∞
f(x) = 
1
x − 5
 is defined for all
x ≠ Correct: Your answer is correct. seenKey

5

 .
 Let
N < 0
 be given. Find
δ > 0
 such that
f(x) = 
1
x − 5
 < N
 whenever
5 − δ < x < 5.
 Let
δ = Correct: Your answer is correct. seenKey

−1/𝘕

 .
 Then for
|5 − δ| < x and x < 5, 
1
|x − 5|
 > 
1
δ
 = Correct: Your answer is correct. seenKey

−𝘕

 ,
 and
1
x − 5
 = − 
1
|x − 5|
 < Correct: Your answer is correct. seenKey

𝘕

 .
 Thus
lim x→5− 
1
x − 5
 = −∞.
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
7. 3/7 points  |  Previous Answers LarCalc12 3.1.027.EP. My Notes
Question Part
Points
Submissions Used
1 2 3 4 5 6 7
1/1 0/1 0/1 1/1 1/1 0/1 0/1
2/100 2/100 2/100 2/100 2/100 1/100 1/100
Total
3/7
 
  • This exercise will develop conceptual understanding.
  • Expanded Problems go beyond a basic exercise to ask students to show the specific steps of their work or to explain the reasoning behind the answers they've provided.
Consider the following function and closed interval.
f(x) = x3 − 
3
2
x2,    [−5, 2]
Find
f '(x).
f '(x) =
3x2−3x
Correct: Your answer is correct. webMathematica generated answer key
Find the critical numbers of f in
(−5, 2)
 and evaluate f at each critical number. (Order your answers from smallest to largest x, then from smallest to largest y.)
(x, y)
=
22
Incorrect: Your answer is incorrect. webMathematica generated answer key
(x, y)
=
28
Incorrect: Your answer is incorrect. webMathematica generated answer key
Evaluate f at each endpoint of
[−5, 2].
left endpoint
(x, y)
=
−5,−162.5
Correct: Your answer is correct. webMathematica generated answer key
right endpoint
(x, y)
=
2,2
Correct: Your answer is correct. webMathematica generated answer key
Find the absolute extrema of the function on the closed interval
[−5, 2].
minimum
(x, y)
=
−∞,−∞
Incorrect: Your answer is incorrect. webMathematica generated answer key
maximum
(x, y)
=
∞,∞
Incorrect: Your answer is incorrect. webMathematica generated answer key
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
8. 2/2 points  |  Previous Answers LarCalc12 2.6.JIT.009. My Notes
Question Part
Points
Submissions Used
1 2
1/1 1/1
2/100 2/100
Total
2/2
 
  • This exercise will address readiness gaps.
  • Just In Time exercises provide timely support by reviewing prerequisites within the context of new concepts throughout the course.
Express x and y in terms of trigonometric ratios of θ.
A right triangle is given.
  • The first side of length x is opposite an unlabeled angle.
  • The second side of length y is opposite the angle θ.
  • The third side of length 28 is opposite the right angle.
x = 
28·cos(θ)
Correct: Your answer is correct. webMathematica generated answer key
y = 
28·sin(θ)
Correct: Your answer is correct. webMathematica generated answer key

Need Help? Watch It

Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
9. 1/1 points  |  Previous Answers LarCalc12 QP.12.003. My Notes
Question Part
Points
Submissions Used
1
1/1
1/100
Total
1/1
 
  • This exercise will address readiness gaps.
  • Quick Prep exercises address readiness gaps by reviewing prerequisite concepts and skills. They can be used early in the course or whenever needed.

Two polynomials P and D are given. Use either synthetic or long division to divide
P(x)
 by
D(x)
 and express the quotient
P(x)
D(x)
 in the form
P(x)
D(x)
 = Q(x) + 
R(x)
D(x)
.
P(x) = x2 + 4x − 8,    D(x) = x + 3
P(x)
D(x)
 =
x+1 + −11x + 3​
Correct: Your answer is correct. webMathematica generated answer key
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
10. 1/1 points  |  Previous Answers calculustp1 2.3.010.defective My Notes
Question Part
Points
Submissions Used
1
1/1
1/100
Total
1/1
 
  • This exercise will address readiness gaps.
  • The Calculus Readiness Bootcamp contains a formative student assessment on prerequisite topics needed for success and targeted learning modules for areas where students struggled.

Evaluate
(f ∘ g)(−3).
f(x) = x + 2;    g(x) = 6x2 − 7
49
Correct: Your answer is correct. webMathematica generated answer key

Solution or Explanation
(f ∘ g)(−3)
=
f(g(−3))
 		     Substitute the given value into
g(x).
g(−3)
=
6(−3)2 − 7
 		     Substitute the function g, evaluated at the given value, into the function expression.
=
f(6(−3)2 − 7)
 		     Follow the Order of Operations rules and evaluate the exponent first.
=
f(6(9) − 7)
 		     Multiply and then subtract.
=
f(47)
 		     Finally, substitute this value into the function f.
=
47 + 2
 		     Now, add.
=
49
Your work in question(s) will also be submitted or saved.
Viewing Saved Work Revert to Last Response
Home My Assignments
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter a number.
Enter an exact number.