WebAssign is not supported for this browser version. Some features or content might not work. System requirements

WebAssign

Welcome, demo@demo

(sign out)

Tuesday, April 1, 2025 06:19 EDT

Home My Assignments Grades Communication Calendar My eBooks

My Cengage Home Notifications Help My Account

Physics - College, section 1, Fall 2019
My Assignments

Thornton and Rex - Modern Physics for S&E 5/e (Homework)

James Finch

Physics - College, section 1, Fall 2019

Instructor: Dr. Friendly

Current Score : 11 / 38

Due : Monday, January 28, 2030 00:00 EST

Last Saved : n/a Saving... ()

Print Assignment

Question

Points

1	2	3	4	5	6	7	8	9	10	11
1/2	2/2	0/4	1/1	1/1	4/4	–/6	–/8	–/1	2/5	–/4

Total

11/38 (28.9%)

Instructions

Now optimized for WebAssign, the updated fifth edition of Modern Physics for Scientists and Engineers offers a contemporary, comprehensive approach with a strong emphasis on applications that illustrate the process behind scientific advances. To help students develop a historical perspective the authors discuss the experiments that led to key discoveries, while the book's sound theoretical foundation in quantum theory helps physics and engineering majors succeed. The fifth edition has been updated to include the latest research in the field and features an updated WebAssign course that includes a mobile-friendly ebook and a variety of assignable questions to enhance the student learning experience. This demo assignment allows many submissions and allows you to try another version of the same question for practice wherever the problem has randomized values.

The answer key and solutions will display after the first submission for demonstration purposes. Instructors can configure these to display after the due date or after a specified number of submissions.

Assignment Submission

For this assignment, you submit answers by question parts. The number of submissions remaining for each question part only changes if you submit or change the answer.

Assignment Scoring

Your last submission is used for your score.

1. 1/2 points | Previous Answers TRModPhys5 2.5.P.019. My Notes

[Understanding the often-complex processes involved in modern physics is essential. To deepen students' understanding of process, solutions have been added to many questions, including this one!]

A rocket ship carrying passengers blasts off to go from New York to Las Vegas, a distance of about 3,600 km.

(a)

How fast (in terms of c) must the rocket ship go to have its own length shortened by 1%?

0.141

(b)

Ignore effects of general relativity and determine how much time (in s) the rocket ship's clock and the ground-based clocks differ when the rocket ship arrives in Las Vegas.

Viewing Saved Work Revert to Last Response

2. 2/2 points | Previous Answers TRModPhys5 3.1.P.004. My Notes

[Physical phenomena can be difficult to simulate in an online environment, which is why figures that appear in WebAssign are always high resolution and come with descriptive alt-text. Hover over the image to see the alt-text displayed.]

An electron entering Thomson's e/m apparatus (see figures below) has an initial velocity (in horizontal direction only) of 5.00 ✕ 10⁶ m/s. Lying around the lab is a permanent horseshoe magnet of strength 1.20 ✕ 10⁻² T, which you would like to use.

A diagram of Thomson's apparatus is shown. The apparatus consists of a horizontal tube which is narrow along its cylindrical left half and, along its right half, flares outward from the center with increasing diameter such that it forms a cone. A circular fluorescent screen is at the right end of the tube, along the surface of the cone's wide base. Two horizontal deflecting plates are shown near the center of tube and oriented such that the negative plate is at the top of the tube while the positive plate is at the bottom. The poles of a horseshoe magnet, also near the center of the tube, are directed at the region between the deflecting plates such that the north pole faces out of the page while the south pole faces into the page. The cathode is on the left end of the tube and the anode is represented by a vertical circular plate (labeled A) oriented such that its planar surface faces the cathode. A high voltage source is underneath the anode and the cathode with the positive end on the right and the negative end on the left. The path of the electron is represented by a horizontal dashed line which continues straight through plate A to a second vertical circular plate labeled B. The electron continues to the right and at the center of the tube, between the deflecting plates and the magnet's poles, the dashed line splits into three diverging paths which continue rightward such that a single paths terminates at either the top, center, or bottom of the screen.

An *x y*-axis is shown. An electron with velocity v₀ moves along the −x-axis toward the right, passes the origin, and moves into the region between two horizontal charged plates of length ℓ. The positive plate is above the negative plate and the region between them is shown to have an electric field (labeled "vector E(down)") which points downward and a magnetic field (labeled "vector B(in)") which points into the page. Once between the plates, the electron's path begins to move up and to the right with increasing slope until it exits the region along a path of constant slope which makes an angle θ with the horizontal. The vertical distance between the electron's entrance point (into the region) and exit point (out of the region) is labeled y.

(a)

What electric field (in V/m) will you need in order to produce zero deflection of the electrons as they travel through the apparatus?

60000

V/m

(b)

When the magnetic field is turned off, but the same electric field remains, how large a deflection (in cm) will occur if the region of nonzero E and B fields is 2 cm long?

8.44

Viewing Saved Work Revert to Last Response

3. 0/4 points | Previous Answers TRModPhys5 4.6.P.039. My Notes

[Modern Physics requires students to approach important subjects from multiple angles. Questions in WebAssign will include several methods for students to input their answer to multi-part problems, including symbolic entry, algebraic questions, and multiple choice. Click into the answer box to display the PhysPad used for symbolic entry.]

If the resolution of a spectrograph is

Δλ = 1.00 ✕ 10⁻¹² m,

would it be able to separate the K_α lines for dysprosium and holmium? Explain.

For the K_α lines, λ is given by the following expression. (Use the following as necessary: Z and R.)

λ =

i12

$webMathematica generated answer key$

Therefore, because the K_α lines for dysprosium and holmium differ (in pm) by a distance of

0.865

pm, which is the specified resolution, the spectrograph be able to separate them.

Viewing Saved Work Revert to Last Response

4. 1/1 points | Previous Answers TRModPhys5 5.SMC.005. My Notes

[These multiple-choice questions may seem standard, but strategic use of these question types in your assignments can provide an opportunity to assess student understanding of key concepts in Modern Physics, as well as to give instructors insight into learning gaps.]

Which of the following statements is most correct about the uncertainty principle?

Our instruments will eventually be able to measure more precisely than the principle presently allows. A particle limited in space can occupy any energy. On large length scales, the uncertainty principle dominates our understanding of the physical world. An electron with some momentum can be trapped into an arbitrarily small box. correct

It is impossible to know exactly both the position and the momentum of a particle simultaneously.

CORRECT: The founding parameters of the uncertainty principle are the position and momentum of a particle proportional to a constant by an inequality. This means that if the value for the position of a particle gets more precise, the value for the momentum gets more imprecise, and vice versa.

Viewing Saved Work Revert to Last Response

5. 1/1 points | Previous Answers TRModPhys5 5.SMC.004. My Notes

The de Broglie wavelength of which of the following objects would be smallest if the objects all had the same momentum?

CORRECT: The de Broglie wavelength of matter is proportional to Planck's constant and inversely proportional to the momentum of the particle. If all the objects had the same momentum, they would all have the same wavelength.

Viewing Saved Work Revert to Last Response

6. 4/4 points | Previous Answers TRModPhys5 6.5.P.029. My Notes

[Derivations are an essential part of a complete physics education. These multi-part questions test student instincts and understanding of the derivation process by stepping them through the process.]

Complete the derivation of

E =

π²ℏ²

n₁²

L₁²

n₂²

L₂²

n₃²

L₃²

by substituting the wave function

ψ(x, y, z) = A sin(k₁x) sin(k₂y) sin(k₃z)

into

−

ℏ²

∇²ψ = Eψ.

Taking the derivatives we find (Use the following as necessary: k₁, k₂, k₃, and ψ.)

∇²ψ =

−(k21+k22+k23)ψ

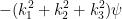
$webMathematica generated answer key$

so the Schrödinger equation becomes (Use the following as necessary: k₁, k₂, k₃, ℏ, m and ψ.)

−

ℏ²

∇²ψ

ℏ22m(k21+k22+k23)ψ

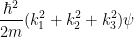
$webMathematica generated answer key$

Eψ

The quantum numbers n_i are related to k_i by (Use the following as necessary: n_i and L_i.)

k_i =

πniLi

$webMathematica generated answer key$

E =

ℏ²π²

n₁²

L₁²

n₂²

L₂²

n₂²

L₂²

What is the origin of the three quantum numbers?

the uncertainty principle the Pauli exclusion principle correct

the three boundary conditions the Schrödinger equation

Solution or Explanation

Taking the derivatives we find

∇²ψ = −(k₁² + k₂² + k₃²)ψ

so the Schrödinger equation becomes

−

ℏ²

∇²ψ =

ℏ²

(k₁² + k₂² + k₃²)ψ = Eψ.

From the boundary conditions

k_i =

n_iπ

L_i

E =

ℏ²π²

n₁²

L₁²

n₂²

L₂²

n₂²

L₂²

The three quantum numbers come directly from the three boundary conditions.

Viewing Saved Work Revert to Last Response

7. –/6 points TRModPhys5 6.7.P.041. My Notes

[Analyzing graphs and data are an essential skill in the study to physics. High resolution figures and alt-text in WebAssign will help your students get a complete picture of the question's simulated data for analysis.]

Compare the wavelength of a particle when it passes a barrier of each of the following heights. Calculate the momentum and kinetic energy for both cases. (Use the following as necessary: m, E, V₀, and h.)

(a)

+V₀,

(see the figure below)

momentum p =

wavelength λ =

kinetic energy K =

(b)

−V₀

where

E > |V₀|

(see the figure below)

A particle of energy E passes in a horizontal line above a potential barrier of height −V₀ on the x V(x) coordinate plane. The diagram is divided into three regions: Region I, Region II, and Region III.

Region I is the region for which x < 0. The particle starts in this region, in the second quadrant. The curve V(x) is horizontal along the x-axis in this region.

Region II is the region for which 0 < x < L. The curve V(x) is horizontal and has a value −V₀ in this region.

Region III is the region for which x > L. The curve V(x) is horizontal along the x-axis in this region.

momentum p =

wavelength λ =

kinetic energy K =

Viewing Saved Work Revert to Last Response

8. –/8 points TRModPhys5 12.7.P.042. My Notes

[In Modern Physics, students will explore concepts from several branches of physics. This question demonstrates the range of subjects covered in this course by assessing conceptual understanding of nuclear and particle physics.]

Find which of the α and β decays are allowed for ²²⁶Ac. (Determine the disintegration energy Q for each decay which is allowed, and calculate the binding energy B against each decay which is not allowed. Enter your answers for each energy in MeV.)

process	Is it allowed?	Q or B
α emission		MeV
β^- emission		MeV
β⁺ emission		MeV
electron capture		MeV

Viewing Saved Work Revert to Last Response

9. –/1 points TRModPhys5 5.7.WA.026. My Notes

[For students studying at home, getting stuck on a problem can be hugely frustrating. Questions like this one come with feedback that guides students toward the correct answer, and a learner-focused solution or explanation to help them understand by stepping through the solution process.]

Determine the probability of finding a quantum particle (restricted to a one-dimensional box of length L), in the interval

0 < x < L/8,

L = 6.23 nm

and the wave function describing the particle is the following.

ψ(x) =

A sin

2πx

for −

< x <

elsewhere

Viewing Saved Work Revert to Last Response

10. 2/5 points | Previous Answers TRModPhys5 8.1.WA.001. My Notes

[This question utilizes the WebAssign ChemPad, a formatting tool for entering standard chemical notation. This question also features feedback and a solution.]

List the electron configuration for all elements from hydrogen through boron. (Use s, p, d ... style notation for subshells.)

Hydrogen

chemPad

Help

1s¹

Correct.

Helium

chemPad

Help

1s²

Correct.

Lithium

chemPad

Help

Beryllium

chemPad

Help

Boron

chemPad

Help

Viewing Saved Work Revert to Last Response

11. –/4 points TRModPhys5 12.5.WA.012.Tutorial. My Notes

[This question, in addition to built-in feedback and solutions, features a Master-It tutorial. Tutorials are multi-part scaffolded questions that will help students progress through difficult processes.]

A plot of binding energy per nucleon

E_b

versus the mass number (A) shows that nuclei with a small mass number have a small binding energy per nucleon, as the mass number increases the binding energy per nucleon increases, and the value for the binding energy per nucleon has a maximum value for nuclei with a mass number around 60. Verify that this is the case by determining the binding energy per nucleon for each of the following four nuclei. (Let the mass of a proton be 1.0078 u, the mass of a neutron be 1.0087 u, the mass of ²H be 2.0141 u, the mass of ⁷Be be 7.0169 u, the mass of ⁶³Cu be 62.9296 u, and the mass of ¹⁰⁷Ag be 106.9051 u. Enter your answers in MeV and to at least three significant figures.)

(a)

²H

MeV

(b)

⁷Be

MeV

(c)

⁶³Cu

MeV

(d)

¹⁰⁷Ag

MeV

Need Help?

Viewing Saved Work Revert to Last Response

Home My Assignments

1	2
1/1	0/1
3/100	2/100

1	2	3	4
0/1	0/1	–/1	–/1
1/100	1/100	0/100	0/100