WebAssign is not supported for this browser version. Some features or content might not work. System requirements

WebAssign

Welcome, demo@demo

(sign out)

Tuesday, April 1, 2025 04:46 EDT

Home My Assignments Grades Communication Calendar My eBooks

My Cengage Home Notifications Help My Account

Physics - College, section 1, Fall 2019
My Assignments

WebAssign - Modern Physics, 1/e (Homework)

James Finch

Physics - College, section 1, Fall 2019

Instructor: Dr. Friendly

Current Score : 5 / 16

Due : Monday, January 28, 2030 00:00 EST

Last Saved : n/a Saving... ()

Print Assignment

Question

Points

1	2	3	4	5	6	7
–/3	–/1	–/1	–/1	–/1	5/5	–/4

Total

5/16 (31.3%)

Instructions

Modern Physics is authored by experienced physics instructors with years of teaching the introductory physics sequence, the new Modern Physics question collection by WebAssign includes more than 500 questions covering every concept in the course, designed to work with any textbook (or no textbook at all).

This sample assignment highlights many of the engaging features of the WebAssign platform as follows:

Question 1 includes a very detailed step-by-step solution to the multi-part question.

Question 2 highlights randomization (figures in red).

Question 4 includes an associated Tutorial which uses the physPad tool for entering a large variety of relevant symbols.

Question 5 uses physPad in the question itself.

Question 6 utilizes chemPad tool for entering symbols required to specify electron configurations. This demo assignment allows many submissions and allows you to try another version of the same question for practice wherever the problem has randomized values.

The answer key and solutions will display after the first submission for demonstration purposes. Instructors can configure these to display after the due date or after a specified number of submissions.

Assignment Submission

For this assignment, you submit answers by question parts. The number of submissions remaining for each question part only changes if you submit or change the answer.

Assignment Scoring

Your last submission is used for your score.

1. –/3 points WAModPhys1 3.P.004. My Notes

As an advanced lab project, you are to develop a lab similar to the original e/m experiment. You find a tube (shown below) which has a filament heated by an AC source, a cathode, anode, collimator, horizontal deflecting plates and a fluorescent screen. You have access to several power supplies and a "U" shaped magnet that produces a 1.19 ✕ 10⁻⁴ T magnetic field. You connect a power supply to the cathode and anode (as shown) and adjust it to 45.0 V. The separation of the deflector plates is 5.00 mm and they are 2.50 cm in length.

(a)

Determine the speed (in m/s) at which electrons enter the region of the crossed electric and magnetic field.

m/s

(b)

Determine the electric potential (in V) which must be applied to the deflecting plates in order for the electrons to pass straight through the region of the crossed electric and magnetic fields.

(c)

If the magnetic field is removed and the electric field kept the same, determine the vertical deflection of the electrons (in mm) as they exit the region of the electric field.

Viewing Saved Work Revert to Last Response

2. –/1 points WAModPhys1 3.P.022. My Notes

What is the maximum kinetic energy in eV of electrons ejected from a certain metal by 440 nm EM radiation, given the work function is 2.27 eV?

Viewing Saved Work Revert to Last Response

3. –/1 points WAModPhys1 5.P.026. My Notes

Determine the probability of finding a quantum particle (restricted to a one-dimensional box of length L), in the interval

0 < x < L/8,

L = 7.00 nm

and the wave function describing the particle is the following.

ψ(x) =

A sin

2πx

for −

< x <

elsewhere

Viewing Saved Work Revert to Last Response

4. –/1 points WAModPhys1 7.P.018.Tutorial. My Notes

When a hydrogen atom is placed in an external magnetic field of 4.60 T, determine the minimum angle (in degrees) between the two possible directions of the spin angular momentum vector.

Tutorial

Viewing Saved Work Revert to Last Response

5. –/1 points WAModPhys1 7.P.025. My Notes

The wave function for hydrogen in the 1s state may be expressed as

ψ(r) = Ae^−r/a₀,

where

A =

πa₀³

Determine the average value for the location of the electron. (Use any variable or symbol stated above as necessary.)

r_avg =

Viewing Saved Work Revert to Last Response

6. 5/5 points | Previous Answers WAModPhys1 8.P.001. My Notes

List the electron configuration for all elements from hydrogen through boron. (Use s, p, d ... style notation for subshells.)

Hydrogen

chemPad

Help

1s¹

Correct.

Helium

chemPad

Help

1s²

Correct.

Lithium

chemPad

Help

1s² 2s¹

Correct.

Beryllium

chemPad

Help

1s² 2s²

Correct.

Boron

chemPad

Help

1s² 2s² 2p¹

Correct.

Solution or Explanation

Acceptable values for the principle quantum number n are

n = 1, 2, 3, 4,

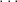
For each value of n, there are n possible values for the orbital angular momentum quantum number ℓ and they are

ℓ = 0, 1, 2, 3, ..., n − 1
ℓ = 0
is associated with s
ℓ = 1
is associated with p
ℓ = 2
is associated with d
ℓ = 3
is associated with f

and so forth.

For each value of ℓ, we may have

2ℓ + 1

values of

m_ℓ

and they range from

−ℓ

+ℓ

in steps of 1 with values of

−ℓ

−ℓ + 1

−ℓ + 2,

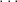
, 0, +1, +2,

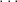
, +ℓ − 1

+ℓ.

For each value of

m_ℓ

there are two acceptable values of

m_s

and they are

m_s = ±1/2.

Applying the above to atoms of hydrogen through boron we have the following.

Hydrogen (with 1 electron) which has quantum numbers

(n, ℓ, m_ℓ, m_s)

equal to

(1, 0, 0, ±1/2)

when in its lowest state. Note that in the absence of a magnetic field, the

m_s = +1/2

state is degenerate with the

m_s = −1/2

state. As a result, we may write

Hydrogen:

1s¹.

Helium (with 2 electrons) which have quantum numbers

(1, 0, 0, +1/2)

and

(1, 0, 0, −1/2)

. Note that the n = 1 shell is now full (all possible quantum numbers associated with n = 1 have been used.) As a result, we may write

Helium:

1s².

Lithium (with 3 electrons). Two of the electrons will fill the n = 1 shell and the third will have quantum numbers

(2, 0, 0, ±1/2)

. Note that in the absence of a magnetic field, the

m_s = +1/2

state is degenerate with the

m_s = −1/2

state. As a result, we may write

Lithium:

1s²2s¹.

Beryllium (with 4 electrons). Two electrons fill the n = 1 shell and the other two have quantum numbers

(2, 0, 0, +1/2)

and

(2, 0, 0, −1/2)

. Note that the n = 2,

ℓ = 0

(or s) subshell is now full (all possible quantum numbers associated with

n = 2 and ℓ = 0

have been used). As a result, we may write

Beryllium:

1s²2s².

Boron: (with 5 electrons). Two electrons fill the n = 1 shell, two fill the

n = 2, ℓ = 0

subshell and the remaining electron goes into the

n = 2, ℓ = 1

subshell. As a result, we may write

Boron:

1s²2s²2p¹.

Viewing Saved Work Revert to Last Response

7. –/4 points WAModPhys1 12.P.012.Tutorial. My Notes

A plot of binding energy per nucleon

E_b

versus the mass number (A) shows that nuclei with a small mass number have a small binding energy per nucleon, as the mass number increases the binding energy per nucleon increases, and the value for the binding energy per nucleon has a maximum value for nuclei with a mass number around 60. Verify that this is the case by determining the binding energy per nucleon for each of the following four nuclei. (Let the mass of a proton be 1.0078 u, the mass of a neutron be 1.0087 u, the mass of ³He be 3.0160 u, the mass of ⁸Li be 8.0225 u, the mass of ⁶²Ni be 61.9283 u, and the mass of ¹¹⁰Cd be 109.9030 u. Enter your answers in MeV and to at least three significant figures.)

(a)

³He

MeV

(b)

⁸Li

MeV

(c)

⁶²Ni

MeV

(d)

¹¹⁰Cd

MeV

Tutorial

Viewing Saved Work Revert to Last Response

Home My Assignments

1	2	3	4	5
1/1	1/1	1/1	1/1	1/1
1/100	1/100	1/100	2/100	1/100

1	2	3
–/1	–/1	–/1
0/100	0/100	0/100

1	2	3	4
–/1	–/1	–/1	–/1
0/100	0/100	0/100	0/100