Every human being has a blood type, and every human being has a DNA sequence. These are examples of functions, where a person is the input and the output is blood type or DNA sequence. These relationships are classified as functions because each person can have one and only one blood type or DNA strand. The difference between these functions is that many people have the same blood type, but DNA is unique to each individual. Can we map backwards? For instance, if you know the blood type, do you know specifically which person it came from? No, but, if you know the DNA sequence, you know exactly to which person it corresponds. When a function has a one-to-one correspondence, like the DNA example, then mapping backwards is possible. The map back is called the inverse function.
Determine Whether a Function Is One-to-One
In Section
3.1, we defined a function as a relationship that maps an input (contained in the domain) to exactly one output (found in the range). Algebraically, each value for

can correspond to only a single value for

. Recall the square, identity, absolute value, and reciprocal functions from our library of functions in Section
3.3.
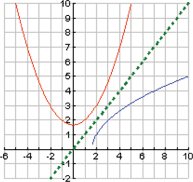
All of the graphs of these functions satisfy the vertical line test. Although the square function and the absolute value function map each value of

to exactly one value for
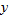
, these two functions map two values of

to the same value for

. For example,
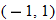
and
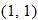
lie on both graphs. The identity and reciprocal functions, on the other hand, map each

to a single value for

, and no two
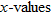
map to the same

. These two functions are examples of
one-to-one functions.
| DEFINITION� |
One-to-One Function |
|
A function  is one-to-one if no two elements in the domain correspond to the same element in the range; that is,
|
|
|
In other words, it is one-to-one if no two inputs map to the same output.
|
EXAMPLE�1�
|
Determining Whether a Function Defined as a Set of Points Is a One-to-One Function |
|
For each of the three relations, determine whether the relation is a function. If it is a function, determine whether it is a one-to-one function.
|
|
|
|
Just as there is a graphical test for functions, the vertical line test, there is a graphical test for one-to-one functions, the
horizontal line test. Note that a horizontal line can be drawn on the square and absolute value functions so that it intersects the graph of each function at two points. The identity and reciprocal functions, however, will intersect a horizontal line in at most only one point. This leads us to the horizontal line test for one-to-one functions.
| DEFINITION� |
Horizontal Line Test |
|
If every horizontal line intersects the graph of a function in at most one point, then the function is classified as a one-to-one function. |
|
|
 �EXAMPLE�2� �EXAMPLE�2�
|
Using the Horizontal Line Test to Determine Whether a Function Is One-to-One |
|
For each of the three relations, determine whether the relation is a function. If it is a function, determine whether it is a one-to-one function. Assume that  is the independent variable and  is the dependent variable.
Solution
|
|
|
|
|
|
|
|
|
(fails vertical line test) |
(passes vertical line test but fails horizontal line test) |
(passes both horizontal and vertical line tests) |
|
|
|
|
Determine whether each of the functions is a one-to-one function.
|
|
|
|
|
|
Another way of writing the definition of a one-to-one function is:
In the Your Turn following Example
2, we found (using the horizontal line test) that

is a one-to-one function, but that
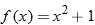
is not a one-to-one function. We can also use this alternative definition to determine algebraically whether a function is one-to-one.
Words |
Math |
State the function. |
|
Let there be two real numbers,  and  , such that  . |
|
Subtract 2 from both sides of the equation. |
|
 is a one-to-one function. |
|
|
Words |
Math |
State the function. |
|
Let there be two real numbers,  and  , such that  . |
|
Subtract 1 from both sides of the equation. |
|
Solve for  . |
|
 is not a one-to-one function. |
|
|
 �EXAMPLE�3� �EXAMPLE�3�
|
Determining Algebraically Whether a Function Is One-to-One |
|
Determine algebraically whether the following functions are one-to-one:
Solution
 |
|
(a)�� |
Find  and  . |
|
Let  . |
|
Add 2 to both sides of the equation. |
|
Divide both sides of the equation by 5. |
|
Take the cube root of both sides of the equation. |
|
Simplify. |
|
|
|
|
|
 |
(b)�� |
Find  and  . |
|
Let  . |
|
Solve the absolute value equation. |
|
|
|
|
|
|
|
|
|
|
Inverse Functions
If a function is one-to-one, then the function maps each

to exactly one

, and no two
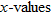
map to the same

. This implies that there is a one-to-one correspondence between the inputs (domain) and outputs (range) of a one-to-one function

. In the special case of a one-to-one function, it would be possible to map from the output (range of

) back to the input (domain of

), and this mapping would also be a function. The function that maps the output back to the input of a function

is called the
inverse function and is denoted

.
A one-to-one function

maps every

in the domain to a unique and distinct corresponding

in the range. Therefore, the inverse function

maps every

back to a unique and distinct

.
The function notations

and

indicate that if the point

satisfies the function, then the point

satisfies the inverse function.
For example, let the function

.
The inverse function undoes whatever the function does. For example, if

, then the function

maps any value

in the domain to a value

in the range. If we want to map backwards or undo the

, we develop a function called the inverse function that takes

as input and maps back to

as output. The inverse function is

. Note that if we input

into the inverse function, the output is

.
| DEFINITION� |
Inverse Function |
|
If  and  denote two one-to-one functions such that
then  is the inverse of the function  . The function 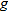 is denoted by  (read “f-inverse”). |
|
|

is used to denote the inverse of

. The

is not used as an exponent and, therefore, does not represent the reciprocal of

:

.
Two properties hold true relating one-to-one functions to their inverses: (1) the range of the function is the domain of the inverse, and the range of the inverse is the domain of the function, and (2) the composite function that results with a function and its inverse (and vice versa) is the identity function

.
|
EXAMPLE�4�
|
Verifying Inverse Functions |
|
Verify that  is the inverse of  .
Solution
Note the relationship between the domain and range of  and  .
|
|
|
|
 �EXAMPLE�5� �EXAMPLE�5�
|
Verifying Inverse Functions with Domain Restrictions |
|
Verify that  , for 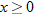 , is the inverse of  .
|
|
|
|
Graphical Interpretation of Inverse Functions
In Example
4, we showed that

is the inverse of

. Let's now investigate the graphs that correspond to the function

and its inverse

.
Note that the point

lies on the function and the point

lies on the inverse. In fact, every point

that lies on the function corresponds to a point

that lies on the inverse.
 |
If the point  is on the function, then the point  is on the inverse. Notice the interchanging of the 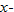 and 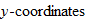 . |
|
|
|
|
Draw the line

on the graph. In general, the point

on the inverse

is the reflection (about

) of the point

on the function

.
In general, if the point

is on the graph of a function, then the point

is on the graph of its inverse.
 �EXAMPLE�6� �EXAMPLE�6�
|
Graphing the Inverse Function |
|
Given the graph of the function  , plot the graph of its inverse  . |
|
|
|
Solution
Because the points  ,  ,  and  lie on the graph of  , then the points  ,  ,  , and  lie on the graph of  . |
|
|
|
|
|
Given the graph of a function  , plot the inverse function. |
|
|
|
|
|
|
|
|
|
We have developed the definition of an inverse function and described properties of inverses. At this point, you should be able to determine whether two functions are inverses of one another. Let's turn our attention to another problem: How do you find the inverse of a function?
Finding the Inverse Function
If the point

lies on the graph of a function, then the point

lies on the graph of the inverse function. The symmetry about the line

tells us that the roles of

and

interchange. Therefore, if we start with every point
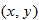
that lies on the graph of a function, then every point

lies on the graph of its inverse. Algebraically, this corresponds to interchanging

and

. Finding the inverse of a finite set of ordered pairs is easy: simply interchange the
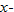
and
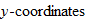
. Earlier, we found that if

, then

. But how do we find the inverse of a function defined by an equation?
Recall the mapping relationship if

is a one-to-one function. This relationship implies that

and

.
Let's use these two identities to find the inverse. Now consider the function defined by

. To find

, we let

, which yields

. Solve for the variable

.
Recall that

, so we have found the inverse to be

. It is customary to write the independent variable as

, so we write the inverse as

. Now that we have found the inverse, let's confirm that the properties

and

hold.
FINDING THE INVERSE OF A FUNCTION |
|
|
Let  be a one-to-one function. Then the following procedure can be used to find the inverse function  if the inverse exists.
The same result is found if we first interchange  and  and then solve for  in terms of  .
Note the following:
|
|
|
|
EXAMPLE�7�
|
The Inverse of a Square Root Function |
|
Find the inverse of the function  . State the domain and range of both  and  .
 |
 �Technology Tip� �Technology Tip� |
|
|
Using a graphing utility, plot  ,  , and  .
Note that the function  and its inverse  are symmetric about the line  .
|
|
|
|
|
Solution
 is a one-to-one function because it passes the horizontal line test. |
|
|
|
(State the domain and range of both  and  .)
 : |
Domain: 
|
Range: 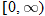
|
 : |
Domain: 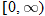
|
Range: 
|
|
|
The inverse of  is  .
 |
Had we ignored the domain and range in Example 7, we would have found the inverse function to be the square function  , which is not a one-to-one function. It is only when we restrict the domain of the square function that we get a one-to-one function. |
|
|
|
|
Check.
 for all  in the domain of  . |
|
 for all  in the domain of  . |
|
Note that the function  and its inverse  for 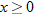 are symmetric about the line  . |
|
|
|
|
|
Find the inverse of the given function. State the domain and range of the inverse function.
|
|
|
|
|
|
|
EXAMPLE�8�
|
A Function That Does Not Have an Inverse Function |
|
Find the inverse of the function  if it exists.
Solution
The function  fails the horizontal line test and therefore is not a one-to-one function. Because  is not a one-to-one function, its inverse function does not exist. |
|
|
|
|
|
|
|
 �EXAMPLE�9� �EXAMPLE�9�
|
Finding the Inverse Function |
|
The function  , is a one-to-one function. Find its inverse.
 |
 �Technology Tip� �Technology Tip� |
|
|
The graphs of  ,  , and  , 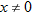 , are shown.
Note that the function  and its inverse  are symmetric about the line  .
|
|
|
|
|
Solution
Step 1 |
Let 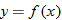 . |
|
Step 2 |
Interchange  and  . |
|
Step 3 |
Solve for  . |
� |
| � |
Multiply the equation by  . |
|
| � |
Eliminate the parentheses. |
|
| � |
Subtract  from both sides. |
|
| � |
Divide the equation by  . |
|
Step 4 |
Let  . |
|
Note any domain restrictions on  . |
|
|
|
 |
The range of the function is equal to the domain of its inverse function. |
|
|
|
|
The inverse of the function  , is  .
|
|
The function  , is a one-to-one function. Find its inverse.
|
|
|
|
|
|
Note in Example
9 that the domain of

is

and the domain of

is

. Therefore, we know that the range of

is

, and the range of

is

.
|
EXAMPLE�10�
|
Finding the Inverse of a Piecewise-Defined Function |
|
The function  , is a one-to-one function. Find its inverse.
Solution
From the graph of  we can make a table with corresponding domain and range values.
Domain of 
|
Range of 
|
|
|
|
|
|
|
|
|
|
|
From this information we can also list domain and range values for  .
Domain of  Range of Range of 
|
Range of  Domain of Domain of 
|
|
|
|
|
|
|
 on  ; find  on  .
Step 1 |
Let 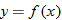 . |
|
Step 2 |
Solve for  in terms of  . |
|
Step 3 |
Solve for  . |
|
Step 4 |
Let  . |
|
|
|
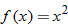 on  ; find  on  .
Step 1 |
Let 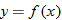 . |
|
Step 2 |
Solve for  in terms of  . |
|
Step 3 |
Solve for  . |
|
Step 4 |
Let  . |
|
Step 5 |
The range of  is 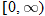
|
|
|
|
Combining the two pieces yields a piecewise-defined inverse function.
|
|
|
|
 �
� can correspond to only a single value for
can correspond to only a single value for  . Recall the square, identity, absolute value, and reciprocal functions from our library of functions in Section 3.3.
. Recall the square, identity, absolute value, and reciprocal functions from our library of functions in Section 3.3. can correspond to only a single value for
can correspond to only a single value for  . Recall the square, identity, absolute value, and reciprocal functions from our library of functions in Section 3.3.
. Recall the square, identity, absolute value, and reciprocal functions from our library of functions in Section 3.3. to exactly one value for
to exactly one value for 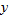 , these two functions map two values of
, these two functions map two values of  to the same value for
to the same value for  . For example,
. For example, 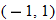 and
and 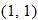 lie on both graphs. The identity and reciprocal functions, on the other hand, map each
lie on both graphs. The identity and reciprocal functions, on the other hand, map each  to a single value for
to a single value for  , and no two
, and no two 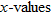 map to the same
map to the same  . These two functions are examples of one-to-one functions.
. These two functions are examples of one-to-one functions.
 to exactly one value for
to exactly one value for 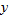 , these two functions map two values of
, these two functions map two values of  to the same value for
to the same value for  . For example,
. For example, 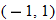 and
and 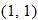 lie on both graphs. The identity and reciprocal functions, on the other hand, map each
lie on both graphs. The identity and reciprocal functions, on the other hand, map each  to a single value for
to a single value for  , and no two
, and no two  map to the same
map to the same  . These two functions are examples of one-to-one functions.
. These two functions are examples of one-to-one functions.
 In the Your Turn following Example 2, we found (using the horizontal line test) that
In the Your Turn following Example 2, we found (using the horizontal line test) that  is a one-to-one function, but that
is a one-to-one function, but that 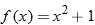 is not a one-to-one function. We can also use this alternative definition to determine algebraically whether a function is one-to-one.
is not a one-to-one function. We can also use this alternative definition to determine algebraically whether a function is one-to-one.

 is a one-to-one function, but that
is a one-to-one function, but that 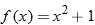 is not a one-to-one function. We can also use this alternative definition to determine algebraically whether a function is one-to-one.
is not a one-to-one function. We can also use this alternative definition to determine algebraically whether a function is one-to-one.
 to exactly one
to exactly one  , and no two
, and no two 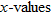 map to the same
map to the same  . This implies that there is a one-to-one correspondence between the inputs (domain) and outputs (range) of a one-to-one function
. This implies that there is a one-to-one correspondence between the inputs (domain) and outputs (range) of a one-to-one function  . In the special case of a one-to-one function, it would be possible to map from the output (range of
. In the special case of a one-to-one function, it would be possible to map from the output (range of  ) back to the input (domain of
) back to the input (domain of  ), and this mapping would also be a function. The function that maps the output back to the input of a function
), and this mapping would also be a function. The function that maps the output back to the input of a function  is called the inverse function and is denoted
is called the inverse function and is denoted  .
. to exactly one
to exactly one  , and no two
, and no two 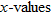 map to the same
map to the same  . This implies that there is a one-to-one correspondence between the inputs (domain) and outputs (range) of a one-to-one function
. This implies that there is a one-to-one correspondence between the inputs (domain) and outputs (range) of a one-to-one function  . In the special case of a one-to-one function, it would be possible to map from the output (range of
. In the special case of a one-to-one function, it would be possible to map from the output (range of  ) back to the input (domain of
) back to the input (domain of  ), and this mapping would also be a function. The function that maps the output back to the input of a function
), and this mapping would also be a function. The function that maps the output back to the input of a function  is called the inverse function and is denoted
is called the inverse function and is denoted  .
. maps every
maps every  in the domain to a unique and distinct corresponding
in the domain to a unique and distinct corresponding  in the range. Therefore, the inverse function
in the range. Therefore, the inverse function  maps every
maps every  back to a unique and distinct
back to a unique and distinct  .
.
 maps every
maps every  in the domain to a unique and distinct corresponding
in the domain to a unique and distinct corresponding  in the range. Therefore, the inverse function
in the range. Therefore, the inverse function  maps every
maps every  back to a unique and distinct
back to a unique and distinct  .
.
 and
and  indicate that if the point
indicate that if the point  satisfies the function, then the point
satisfies the function, then the point  satisfies the inverse function.
satisfies the inverse function. and
and  indicate that if the point
indicate that if the point  satisfies the function, then the point
satisfies the function, then the point  satisfies the inverse function.
satisfies the inverse function. .
.
 .
.
 , then the function
, then the function  maps any value
maps any value  in the domain to a value
in the domain to a value  in the range. If we want to map backwards or undo the
in the range. If we want to map backwards or undo the  , we develop a function called the inverse function that takes
, we develop a function called the inverse function that takes  as input and maps back to
as input and maps back to  as output. The inverse function is
as output. The inverse function is  . Note that if we input
. Note that if we input  into the inverse function, the output is
into the inverse function, the output is  .
.
 is used to denote the inverse of
is used to denote the inverse of  . The
. The  is not used as an exponent and, therefore, does not represent the reciprocal of
is not used as an exponent and, therefore, does not represent the reciprocal of  :
:  .
.
 , then the function
, then the function  maps any value
maps any value  in the domain to a value
in the domain to a value  in the range. If we want to map backwards or undo the
in the range. If we want to map backwards or undo the  , we develop a function called the inverse function that takes
, we develop a function called the inverse function that takes  as input and maps back to
as input and maps back to  as output. The inverse function is
as output. The inverse function is  . Note that if we input
. Note that if we input  into the inverse function, the output is
into the inverse function, the output is  .
.
 is used to denote the inverse of
is used to denote the inverse of  . The
. The  is not used as an exponent and, therefore, does not represent the reciprocal of
is not used as an exponent and, therefore, does not represent the reciprocal of  :
:  .
.
 .
.
 .
.
 is the inverse of
is the inverse of  . Let's now investigate the graphs that correspond to the function
. Let's now investigate the graphs that correspond to the function  and its inverse
and its inverse  .
.
 lies on the function and the point
lies on the function and the point  lies on the inverse. In fact, every point
lies on the inverse. In fact, every point  that lies on the function corresponds to a point
that lies on the function corresponds to a point  that lies on the inverse.
that lies on the inverse.
 is the inverse of
is the inverse of  . Let's now investigate the graphs that correspond to the function
. Let's now investigate the graphs that correspond to the function  and its inverse
and its inverse  .
.


 lies on the function and the point
lies on the function and the point  lies on the inverse. In fact, every point
lies on the inverse. In fact, every point  that lies on the function corresponds to a point
that lies on the function corresponds to a point  that lies on the inverse.
that lies on the inverse.
 on the graph. In general, the point
on the graph. In general, the point  on the inverse
on the inverse  is the reflection (about
is the reflection (about  ) of the point
) of the point  on the function
on the function  .
. on the graph. In general, the point
on the graph. In general, the point  on the inverse
on the inverse  is the reflection (about
is the reflection (about  ) of the point
) of the point  on the function
on the function  .
. is on the graph of a function, then the point
is on the graph of a function, then the point  is on the graph of its inverse.
is on the graph of its inverse. is on the graph of a function, then the point
is on the graph of a function, then the point  is on the graph of its inverse.
is on the graph of its inverse. lies on the graph of a function, then the point
lies on the graph of a function, then the point  lies on the graph of the inverse function. The symmetry about the line
lies on the graph of the inverse function. The symmetry about the line  tells us that the roles of
tells us that the roles of  and
and  interchange. Therefore, if we start with every point
interchange. Therefore, if we start with every point 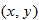 that lies on the graph of a function, then every point
that lies on the graph of a function, then every point  lies on the graph of its inverse. Algebraically, this corresponds to interchanging
lies on the graph of its inverse. Algebraically, this corresponds to interchanging  and
and  . Finding the inverse of a finite set of ordered pairs is easy: simply interchange the
. Finding the inverse of a finite set of ordered pairs is easy: simply interchange the 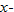 and
and 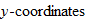 . Earlier, we found that if
. Earlier, we found that if  , then
, then  . But how do we find the inverse of a function defined by an equation?
. But how do we find the inverse of a function defined by an equation? lies on the graph of a function, then the point
lies on the graph of a function, then the point  lies on the graph of the inverse function. The symmetry about the line
lies on the graph of the inverse function. The symmetry about the line  tells us that the roles of
tells us that the roles of  and
and  interchange. Therefore, if we start with every point
interchange. Therefore, if we start with every point 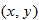 that lies on the graph of a function, then every point
that lies on the graph of a function, then every point  lies on the graph of its inverse. Algebraically, this corresponds to interchanging
lies on the graph of its inverse. Algebraically, this corresponds to interchanging  and
and  . Finding the inverse of a finite set of ordered pairs is easy: simply interchange the
. Finding the inverse of a finite set of ordered pairs is easy: simply interchange the 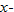 and
and  . Earlier, we found that if
. Earlier, we found that if  , then
, then  . But how do we find the inverse of a function defined by an equation?
. But how do we find the inverse of a function defined by an equation? is a one-to-one function. This relationship implies that
is a one-to-one function. This relationship implies that  and
and  .
.
 . To find
. To find  , we let
, we let  , which yields
, which yields  . Solve for the variable
. Solve for the variable  .
. is a one-to-one function. This relationship implies that
is a one-to-one function. This relationship implies that  and
and  .
.
 . To find
. To find  , we let
, we let  , which yields
, which yields  . Solve for the variable
. Solve for the variable  .
. , so we have found the inverse to be
, so we have found the inverse to be  . It is customary to write the independent variable as
. It is customary to write the independent variable as  , so we write the inverse as
, so we write the inverse as  . Now that we have found the inverse, let's confirm that the properties
. Now that we have found the inverse, let's confirm that the properties  and
and  hold.
hold.

 , so we have found the inverse to be
, so we have found the inverse to be  . It is customary to write the independent variable as
. It is customary to write the independent variable as  , so we write the inverse as
, so we write the inverse as  . Now that we have found the inverse, let's confirm that the properties
. Now that we have found the inverse, let's confirm that the properties  and
and  hold.
hold.

 is
is  and the domain of
and the domain of  is
is  . Therefore, we know that the range of
. Therefore, we know that the range of  is
is  , and the range of
, and the range of  is
is  .
. is
is  and the domain of
and the domain of  is
is  . Therefore, we know that the range of
. Therefore, we know that the range of  is
is  , and the range of
, and the range of  is
is  .
.





























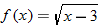















 . Determine the inverse function
. Determine the inverse function  . What does the inverse function represent?
. What does the inverse function represent? . Determine the inverse function
. Determine the inverse function  . What does the inverse function represent?
. What does the inverse function represent? per boat for the first 10 boats and
per boat for the first 10 boats and  for each additional boat. Find the cost function
for each additional boat. Find the cost function  as a function of the number of boats the club enters
as a function of the number of boats the club enters  . Find the inverse function that will yield how many boats the club can enter as a function of how much money it will raise.
. Find the inverse function that will yield how many boats the club can enter as a function of how much money it will raise. per minute for the first 10 minutes of a long-distance phone call and
per minute for the first 10 minutes of a long-distance phone call and  per minute every minute after that. Find the cost function
per minute every minute after that. Find the cost function  as a function of the length of the phone call in minutes
as a function of the length of the phone call in minutes  . Suppose you buy a “prepaid” phone card that is planned for a single call. Find the inverse function that determines how many minutes you can talk as a function of how much you prepaid.
. Suppose you buy a “prepaid” phone card that is planned for a single call. Find the inverse function that determines how many minutes you can talk as a function of how much you prepaid. per hour and the weekly number of hours worked per week
per hour and the weekly number of hours worked per week  varies. If Target withholds
varies. If Target withholds  of his earnings for taxes and Social Security, write a function
of his earnings for taxes and Social Security, write a function  that expresses the student's take-home pay each week. Find the inverse function
that expresses the student's take-home pay each week. Find the inverse function  . What does the inverse function tell you?
. What does the inverse function tell you? per hour for the first 40 hours per week and time and a half for overtime. Write a piecewise-defined function that represents your weekly earnings
per hour for the first 40 hours per week and time and a half for overtime. Write a piecewise-defined function that represents your weekly earnings  as a function of the number of hours worked
as a function of the number of hours worked  . Find the inverse function
. Find the inverse function  . What does the inverse function tell you?
. What does the inverse function tell you? where
where  represents that patient's temperature in degrees Fahrenheit and
represents that patient's temperature in degrees Fahrenheit and  represents the time of day in hours measured from 12:00 a.m. (midnight).
represents the time of day in hours measured from 12:00 a.m. (midnight).
 represents that patient's temperature in degrees Fahrenheit and
represents that patient's temperature in degrees Fahrenheit and  represents the time of day in hours measured from 12:00 a.m. (midnight).
represents the time of day in hours measured from 12:00 a.m. (midnight). .
. .
. found in Exercise 72.
found in Exercise 72. ?
?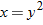 a one-to-one function?
a one-to-one function?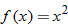 , find the inverse function
, find the inverse function  .
. and
and  .
.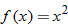 is
is  .
. , find the inverse function
, find the inverse function  , and state the domain restrictions on
, and state the domain restrictions on  .
. is
is  .
. is
is  .
. .
. has an inverse. If the function lies in quadrant II, then its inverse lies in quadrant IV.
has an inverse. If the function lies in quadrant II, then its inverse lies in quadrant IV.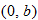 is the
is the  of a one-to-one function
of a one-to-one function  , what is the
, what is the  of the inverse
of the inverse  ?
? is the
is the  of a one-to-one function
of a one-to-one function  , what is the
, what is the  of the inverse
of the inverse  ?
? .
.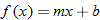 a one-to-one function?
a one-to-one function?






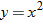
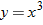







 and
and  , such that
, such that  .
.




 is
is 

 and
and  .
.













 denote two one-to-one functions such that
denote two one-to-one functions such that

 is denoted by
is denoted by 

 is the inverse of
is the inverse of  .
.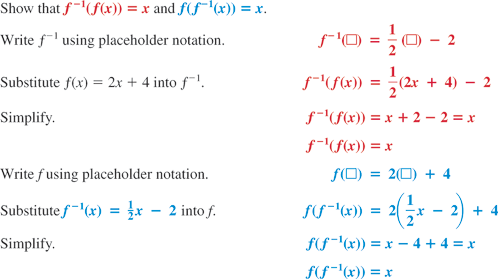
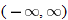
 , for
, for 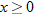 , is the inverse of
, is the inverse of  .
.
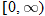




















 ,
,  and
and  lie on the graph of
lie on the graph of  , then the points
, then the points  ,
,  , and
, and  lie on the graph of
lie on the graph of  .
.





 . State the domain and range of both
. State the domain and range of both 
 �Technology Tip�
�Technology Tip� ,
,  , and
, and  .
.





 .
.
 , which is not a one-to-one function. It is only when we restrict the domain of the square function that we get a one-to-one function.
, which is not a one-to-one function. It is only when we restrict the domain of the square function that we get a one-to-one function.

 for
for 

 , Domain:
, Domain: 
 , Domain:
, Domain: 
 if it exists.
if it exists.
 , is a one-to-one function. Find its inverse.
, is a one-to-one function. Find its inverse.
 ,
,  , and
, and  ,
, 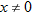 , are shown.
, are shown.


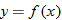 .
.

 .
.

 from both sides.
from both sides.

 .
.
 .
. .
.
 , is a one-to-one function. Find its inverse.
, is a one-to-one function. Find its inverse.
 , is a one-to-one function. Find its inverse.
, is a one-to-one function. Find its inverse.


 on
on 



 ; find
; find 




 are repeated.
are repeated. range of
range of  range of
range of 

 .
.


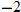 .
. all map to 1 in the range, for instance.
all map to 1 in the range, for instance.
 are on the graph.
are on the graph.




 lie on the graph.
lie on the graph.



 .
.
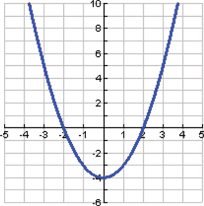




 .
. .
.













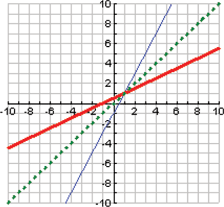














 for
for 
 .
.

 for
for 
 .
.
 for
for 
 .
.
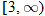
 for
for 
 .
.


 for
for 
 .
.


 for
for 
 .
.

 for
for 
 .
.


 for
for 
 .
.

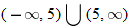

 for
for 
 .
.




 is merely a reflection of this graph over the origin.
is merely a reflection of this graph over the origin.


 ; this now represents degrees Fahrenheit being turned into degrees Celsius.
; this now represents degrees Fahrenheit being turned into degrees Celsius. for
for 
 . The inverse function represents the conversion from degrees Fahrenheit to degrees Celsius.
. The inverse function represents the conversion from degrees Fahrenheit to degrees Celsius.
 . The cost function is
. The cost function is

 , we calculate the inverse of each piece separately:
, we calculate the inverse of each piece separately: : Solve
: Solve  for
for  . So,
. So,  , for
, for  .
. : Solve
: Solve  for
for  . So,
. So,  , for
, for  .
.
 tells you how many hours the student will have to work to bring home
tells you how many hours the student will have to work to bring home  . Then, the take home pay is given by
. Then, the take home pay is given by

 , solve
, solve  for
for  . So,
. So,  .
.
 . For the range, note that
. For the range, note that  is always increasing (being a translate of
is always increasing (being a translate of  ) and so, its minimum is
) and so, its minimum is  and its maximum is
and its maximum is  . So, the range is the approximate interval
. So, the range is the approximate interval  .
.
 is the range of
is the range of 
 and
and  lie on the graph of the function.
lie on the graph of the function.
 and
and  lie on the graph of the inverse.
lie on the graph of the inverse.


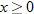 . Then, the calculation will be valid.
. Then, the calculation will be valid.


 .
. implies that the horizontal line test is violated.
implies that the horizontal line test is violated. . Then,
. Then,  also.
also.
 since the
since the 
 . The portion in Quadrant I is given by
. The portion in Quadrant I is given by


 . The domain and range of both are
. The domain and range of both are  .
.
 (that is, while the graph of
(that is, while the graph of 









 , then they would have been.
, then they would have been.