Two different functions can be combined using mathematical operations such as addition, subtraction, multiplication, and division. Also, there is an operation on functions called composition, which can be thought of as a function of a function. When we combine functions, we do so algebraically. Special attention must be paid to the domain and range of the combined functions.
Adding, Subtracting, Multiplying, and Dividing Functions
Consider the two functions
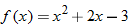
and
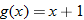
. The domain of both of these functions is the set of all real numbers. Therefore, we can add, subtract, or multiply these functions for any real number

.
The result is in fact a new function, which we denote:
The result is in fact a new function, which we denote:
The result is in fact a new function, which we denote:
Although both

and

are defined for all real numbers

, we must restrict

so that
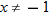
to form the quotient
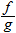
.
The result is in fact a new function, which we denote:
Two functions can be added, subtracted, and multiplied. The resulting function domain is therefore the intersection of the domains of the two functions. However, for division, any value of

(input) that makes the denominator equal to zero must be eliminated from the domain.
The previous examples involved polynomials. The domain of any polynomial is the set of all real numbers. Adding, subtracting, and multiplying polynomials result in other polynomials, which have domains of all real numbers. Let's now investigate operations applied to functions that have a restricted domain.
The domain of the sum function, difference function, or product function is the
intersection of the individual domains of the two functions. The quotient function has a similar domain in that it is the intersection of the two domains. However, any values that make the denominator zero must also be eliminated.
Function |
Notation |
Domain |
Sum |
|
|
Difference |
|
|
Product |
|
|
Quotient |
|
|
|
|
We can think of this in the following way: Any number that is in the domain of
both the functions is in the domain of the combined function. The exception to this is the quotient function, which also eliminates values that make the denominator equal to zero.
|
EXAMPLE�1�
|
Operations on Functions: Determining Domains of New Functions |
|
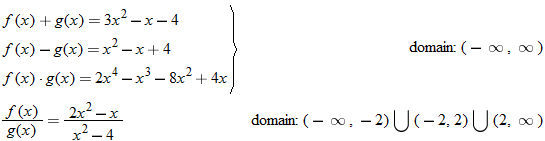
For the functions 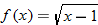 and 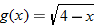 , determine the sum function, difference function, product function, and quotient function. State the domain of these four new functions.
 |
 �Technology Tip �Technology Tip |
|
|
|
|
|
Solution
Sum function: |
|
Difference function: |
|
Product function: |
|
Quotient function: |
|
|
|
The domain of the square root function is determined by setting the argument under the radical greater than or equal to zero.
The domain of the sum, difference, and product functions is
The quotient function has the additional constraint that the denominator cannot be zero. This implies that 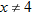 , so the domain of the quotient function is 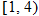 .
|
|
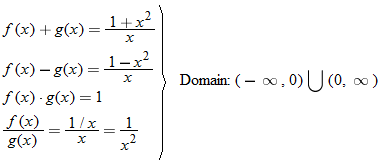
Given the function 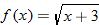 and 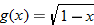 , find 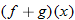 and state its domain.
|
|
|
|
|
|
 �EXAMPLE�2� �EXAMPLE�2�
|
Quotient Function and Domain Restrictions |
|
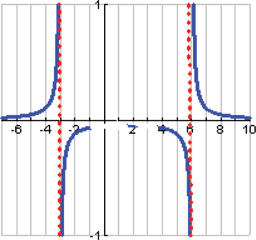
Given the functions 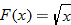 and 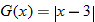 , find the quotient function, 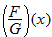 , and state its domain.
 |
 �Technology Tip� �Technology Tip� |
|
|
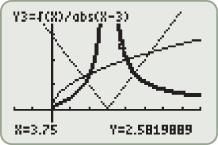
The graphs of 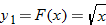 , 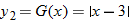 , and 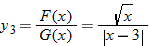 are shown.
|
|
|
|
|
Solution
The quotient function is written as
Domain of 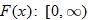
|
Domain of 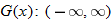
|
|
|
The real numbers that are in both the domain for 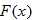 and the domain for 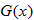 are represented by the intersection 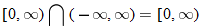 . Also, the denominator of the quotient function is equal to zero when 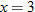 , so we must eliminate this value from the domain.
|
|
For the functions given in Example 2, determine the quotient function 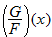 , and state its domain.
|
|
|
|
|
|
Composition of Functions
Recall that a function maps every element in the domain to exactly one corresponding element in the range as shown in the figure below.
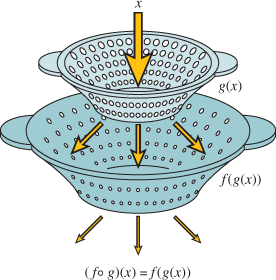
Suppose there is a sales rack of clothes in a department store. Let

correspond to the original price of each item on the rack. These clothes have recently been marked down
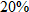
. Therefore, the function
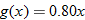
represents the current sale price of each item. You have been invited to a special sale that lets you take
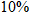
off the current sale price and an additional

off every item at checkout. The function
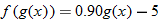
determines the checkout price. Note that the output of the function

is the input of the function

as shown in the figure below.
This is an example of a
composition of functions, when the output of one function is the input of another function. It is commonly referred to as a function of a function.
An algebraic example of this is the function
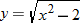
. Suppose we let
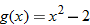
and
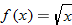
. Recall that the independent variable in function notation is a placeholder. Since
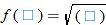
, then
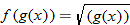
. Substituting the expression for

, we find
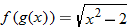
. The function
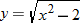
is said to be a composite function,
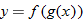
.
Note that the domain of

is the set of all real numbers, and the domain of

is the set of all nonnegative numbers. The domain of a composite function is the set of all

such that

is in the domain of

. For instance, in the composite function
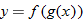
, we know that the allowable inputs into

are all numbers greater than or equal to zero. Therefore, we restrict the outputs of
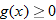
and find the corresponding
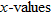
. Those
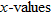
are the only allowable inputs and constitute the domain of the composite function
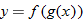
.
The symbol that represents composition of functions is a small open circle; thus
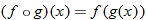
and is read aloud as “

of

.” It is important not to confuse this with the multiplication sign:
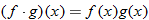
.
Given two functions  and  , there are two composite functions that can be formed.
Notation |
Words |
Definition |
Domain |
|
 composed with 
|
|
The set of all real numbers  in the domain of  such that  is also in the domain of  . |
|
 composed with 
|
|
The set of all real numbers  in the domain of  such that  is also in the domain of  . |
|
|
|
|
|
It is important to realize that there are two “filters” that allow certain values of

into the domain. The first filter is

. If

is not in the domain of

, it cannot be in the domain of
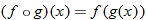
. Of those values for

that are in the domain of

, only some pass through, because we restrict the output of

to values that are allowable as input into

. This adds an additional filter.
The domain of
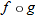
is always a subset of the domain of

, and the range of
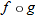
is always a subset of the range of

.
 |
The domain of 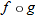 is always a subset of the domain of  , and the range of 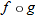 is always a subset of the range of  . |
|
|
|
|
 �EXAMPLE�3� �EXAMPLE�3�
|
Finding a Composite Function |
|
Given the functions 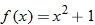 and 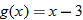 , find 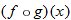 .
 |
 �Technology Tip �Technology Tip |
|
|
|
|
|
Solution
Write  using placeholder notation. |
|
Express the composite function 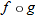 . |
|
Substitute 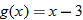 into  . |
|
Eliminate the parentheses on the right side. |
|
|
|
|
|
|
Given the functions in Example 3, find 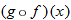 .
|
|
|
|
|
|
 �EXAMPLE�4� �EXAMPLE�4�
|
Determining the Domain of a Composite Function |
|
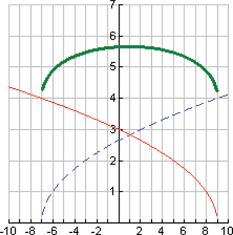
Given the functions 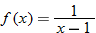 and 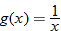 , determine 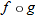 , and state its domain.
 |
 �Technology Tip� �Technology Tip� |
|
|
The graphs of 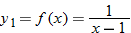 , 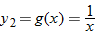 , and 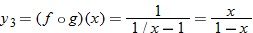 are shown.
|
|
|
|
|
Solution
Write  using placeholder notation. |
|
Express the composite function 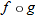 . |
|
Substitute 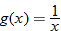 into  . |
|
Multiply the right side by 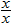 . |
|
|
|
What is the domain of 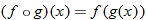 ? By inspecting the final result of 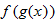 , we see that the denominator is zero when  . Therefore, 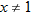 . Are there any other values for  that are not allowed? The function  has the domain 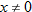 ; therefore we must also exclude zero.
The domain of 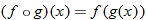 excludes  and  or, in interval notation,
|
|
For the functions  and  given in Example 4, determine the composite function 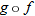 and state its domain.
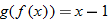 . Domain of 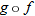 is 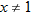 , or in interval notation, 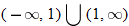 .
|
|
|
|
|
|
The domain of the composite function cannot always be determined by examining the final form of
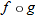
.
 |
The domain of the composite function cannot always be determined by examining the final form of 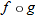 . |
|
|
|
|
|
EXAMPLE�5�
|
Determining the Domain of a Composite Function (Without Finding the Composite Function) |
|
Let 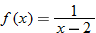 and 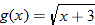 . Find the domain of 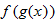 . Do not find the composite function.
Solution
Find the domain of  . |
|
Find the range of  . |
|
|
|
In 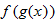 , the output of  becomes the input for  . Since the domain of  is the set of all real numbers except 2, we eliminate any values of  in the domain of  that correspond to 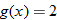 .
Let 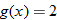 . |
|
Square both sides. |
|
Solve for  . |
|
|
|
Eliminate  from the domain of  , 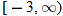 .
State the domain of 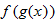 . |
|
|
|
|
|
|
|
 �EXAMPLE�6� �EXAMPLE�6�
|
Evaluating a Composite Function |
|
Given the functions 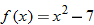 and 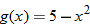 , evaluate:
Solution
One way of evaluating these composite functions is to calculate the two individual composites in terms of  : 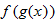 and 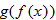 . Once those functions are known, the values can be substituted for  and evaluated. Another way of proceeding is as follows:
 |
|
(a)�� |
Write the desired quantity. |
|
Find the value of the inner function  . |
|
Substitute 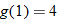 into  . |
|
Evaluate 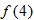 . |
|
|
|
|
 |
(b)�� |
Write the desired quantity. |
|
Find the value of the inner function  . |
|
Substitute 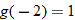 into  . |
|
Evaluate 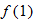 . |
|
|
|
|
 |
(c)�� |
Write the desired quantity. |
|
Find the value of the inner function  . |
|
Substitute 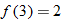 into  . |
|
Evaluate 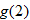 . |
|
|
|
|
 |
(d)�� |
Write the desired quantity. |
|
Find the value of the inner function  . |
|
Substitute 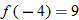 into  . |
|
Evaluate 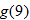 . |
|
|
|
|
|
|
|
Given the functions 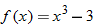 and 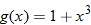 , evaluate 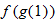 and 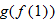 .
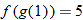 and 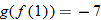
|
|
|
|
|
|
3.4.2.1�Application Problems
Recall the example at the beginning of this chapter regarding the clothes that are on sale. Often, real-world applications are modeled with composite functions. In the clothes example,

is the original price of each item. The first function maps its input (original price) to an output (sale price). The second function maps its input (sale price) to an output (checkout price). Example
7 is another real-world application of composite functions.
Three temperature scales are commonly used:
The equations that relate these temperature scales are
|
EXAMPLE�7�
|
Applications Involving Composite Functions |
|
Determine degrees Fahrenheit as a function of kelvins.
Solution
Degrees Fahrenheit is a function of degrees Celsius. |
|
Now substitute 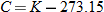 into the equation for 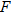 . |
|
Simplify. |
|
| � |
|
|
|
|
|
|
|
 �
�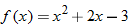 and
and 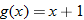 . The domain of both of these functions is the set of all real numbers. Therefore, we can add, subtract, or multiply these functions for any real number
. The domain of both of these functions is the set of all real numbers. Therefore, we can add, subtract, or multiply these functions for any real number  .
.
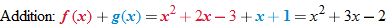 The result is in fact a new function, which we denote:
The result is in fact a new function, which we denote:
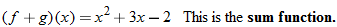
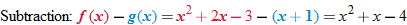 The result is in fact a new function, which we denote:
The result is in fact a new function, which we denote:
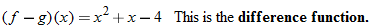
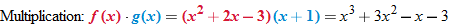 The result is in fact a new function, which we denote:
The result is in fact a new function, which we denote:
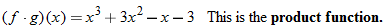 Although both
Although both  and
and  are defined for all real numbers
are defined for all real numbers  , we must restrict
, we must restrict  so that
so that 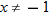 to form the quotient
to form the quotient 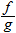 .
.
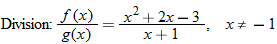 The result is in fact a new function, which we denote:
The result is in fact a new function, which we denote:
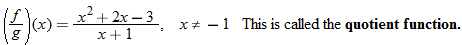
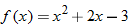 and
and 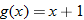 . The domain of both of these functions is the set of all real numbers. Therefore, we can add, subtract, or multiply these functions for any real number
. The domain of both of these functions is the set of all real numbers. Therefore, we can add, subtract, or multiply these functions for any real number  .
.
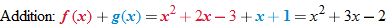
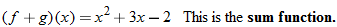
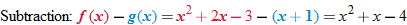
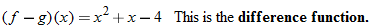
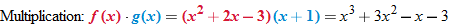
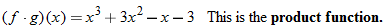
 and
and  are defined for all real numbers
are defined for all real numbers  , we must restrict
, we must restrict  so that
so that 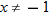 to form the quotient
to form the quotient 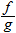 .
.
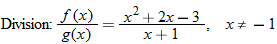
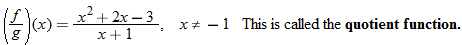
 (input) that makes the denominator equal to zero must be eliminated from the domain.
(input) that makes the denominator equal to zero must be eliminated from the domain. (input) that makes the denominator equal to zero must be eliminated from the domain.
(input) that makes the denominator equal to zero must be eliminated from the domain. correspond to the original price of each item on the rack. These clothes have recently been marked down
correspond to the original price of each item on the rack. These clothes have recently been marked down 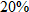 . Therefore, the function
. Therefore, the function 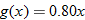 represents the current sale price of each item. You have been invited to a special sale that lets you take
represents the current sale price of each item. You have been invited to a special sale that lets you take 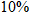 off the current sale price and an additional
off the current sale price and an additional  off every item at checkout. The function
off every item at checkout. The function 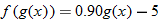 determines the checkout price. Note that the output of the function
determines the checkout price. Note that the output of the function  is the input of the function
is the input of the function  as shown in the figure below.
as shown in the figure below.
 correspond to the original price of each item on the rack. These clothes have recently been marked down
correspond to the original price of each item on the rack. These clothes have recently been marked down 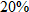 . Therefore, the function
. Therefore, the function 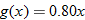 represents the current sale price of each item. You have been invited to a special sale that lets you take
represents the current sale price of each item. You have been invited to a special sale that lets you take 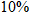 off the current sale price and an additional
off the current sale price and an additional  off every item at checkout. The function
off every item at checkout. The function 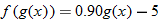 determines the checkout price. Note that the output of the function
determines the checkout price. Note that the output of the function  is the input of the function
is the input of the function  as shown in the figure below.
as shown in the figure below.
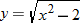 . Suppose we let
. Suppose we let 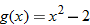 and
and 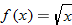 . Recall that the independent variable in function notation is a placeholder. Since
. Recall that the independent variable in function notation is a placeholder. Since 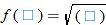 , then
, then 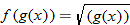 . Substituting the expression for
. Substituting the expression for  , we find
, we find 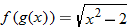 . The function
. The function 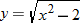 is said to be a composite function,
is said to be a composite function, 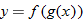 .
.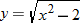 . Suppose we let
. Suppose we let 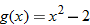 and
and 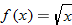 . Recall that the independent variable in function notation is a placeholder. Since
. Recall that the independent variable in function notation is a placeholder. Since 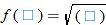 , then
, then 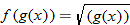 . Substituting the expression for
. Substituting the expression for  , we find
, we find 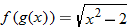 . The function
. The function 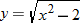 is said to be a composite function,
is said to be a composite function, 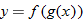 .
. is the set of all real numbers, and the domain of
is the set of all real numbers, and the domain of  is the set of all nonnegative numbers. The domain of a composite function is the set of all
is the set of all nonnegative numbers. The domain of a composite function is the set of all  such that
such that  is in the domain of
is in the domain of  . For instance, in the composite function
. For instance, in the composite function 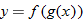 , we know that the allowable inputs into
, we know that the allowable inputs into  are all numbers greater than or equal to zero. Therefore, we restrict the outputs of
are all numbers greater than or equal to zero. Therefore, we restrict the outputs of 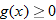 and find the corresponding
and find the corresponding 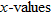 . Those
. Those 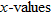 are the only allowable inputs and constitute the domain of the composite function
are the only allowable inputs and constitute the domain of the composite function 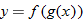 .
. is the set of all real numbers, and the domain of
is the set of all real numbers, and the domain of  is the set of all nonnegative numbers. The domain of a composite function is the set of all
is the set of all nonnegative numbers. The domain of a composite function is the set of all  such that
such that  is in the domain of
is in the domain of  . For instance, in the composite function
. For instance, in the composite function 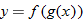 , we know that the allowable inputs into
, we know that the allowable inputs into  are all numbers greater than or equal to zero. Therefore, we restrict the outputs of
are all numbers greater than or equal to zero. Therefore, we restrict the outputs of 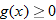 and find the corresponding
and find the corresponding 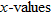 . Those
. Those 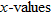 are the only allowable inputs and constitute the domain of the composite function
are the only allowable inputs and constitute the domain of the composite function 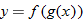 .
.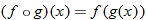 and is read aloud as “
and is read aloud as “ of
of  .” It is important not to confuse this with the multiplication sign:
.” It is important not to confuse this with the multiplication sign: 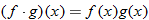 .
.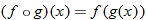 and is read aloud as “
and is read aloud as “ of
of  .” It is important not to confuse this with the multiplication sign:
.” It is important not to confuse this with the multiplication sign: 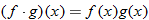 .
. into the domain. The first filter is
into the domain. The first filter is  . If
. If  is not in the domain of
is not in the domain of  , it cannot be in the domain of
, it cannot be in the domain of 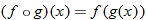 . Of those values for
. Of those values for  that are in the domain of
that are in the domain of  , only some pass through, because we restrict the output of
, only some pass through, because we restrict the output of  to values that are allowable as input into
to values that are allowable as input into  . This adds an additional filter.
. This adds an additional filter. into the domain. The first filter is
into the domain. The first filter is  . If
. If  is not in the domain of
is not in the domain of  , it cannot be in the domain of
, it cannot be in the domain of 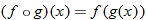 . Of those values for
. Of those values for  that are in the domain of
that are in the domain of  , only some pass through, because we restrict the output of
, only some pass through, because we restrict the output of  to values that are allowable as input into
to values that are allowable as input into  . This adds an additional filter.
. This adds an additional filter.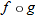 is always a subset of the domain of
is always a subset of the domain of  , and the range of
, and the range of 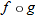 is always a subset of the range of
is always a subset of the range of  .
.
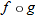 is always a subset of the domain of
is always a subset of the domain of  , and the range of
, and the range of 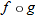 is always a subset of the range of
is always a subset of the range of  .
.
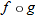 .
.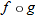 .
. is the original price of each item. The first function maps its input (original price) to an output (sale price). The second function maps its input (sale price) to an output (checkout price). Example 7 is another real-world application of composite functions.
is the original price of each item. The first function maps its input (original price) to an output (sale price). The second function maps its input (sale price) to an output (checkout price). Example 7 is another real-world application of composite functions. is the original price of each item. The first function maps its input (original price) to an output (sale price). The second function maps its input (sale price) to an output (checkout price). Example 7 is another real-world application of composite functions.
is the original price of each item. The first function maps its input (original price) to an output (sale price). The second function maps its input (sale price) to an output (checkout price). Example 7 is another real-world application of composite functions.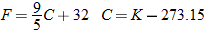
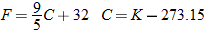
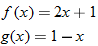
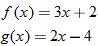
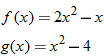
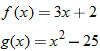
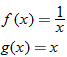
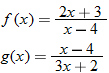
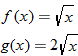
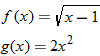
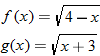
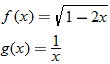
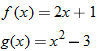
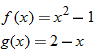
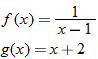
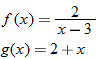
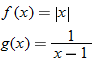
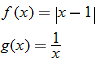
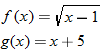
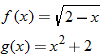
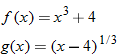
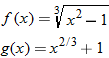
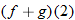
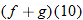
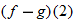
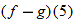
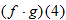
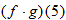
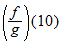
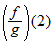
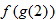
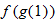
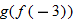
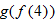
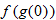
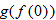
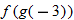
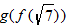
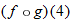
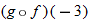
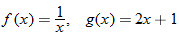
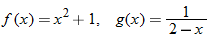
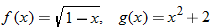
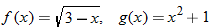
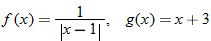
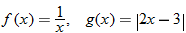
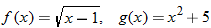
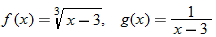
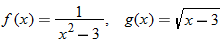
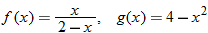
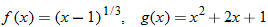
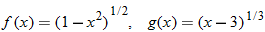
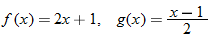
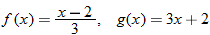
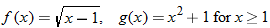
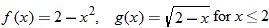
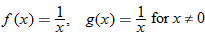
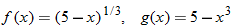
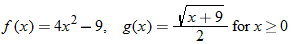
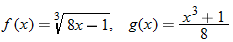
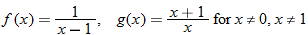
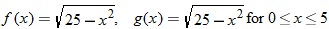
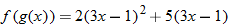
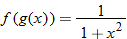
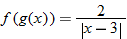
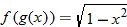
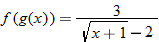
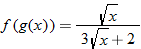
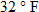 and
and 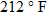 .
.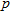 and the number of units for sale
and the number of units for sale  are related by the demand equation:
are related by the demand equation:
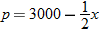
 of producing
of producing  items is governed by the equation
items is governed by the equation
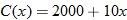
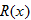 generated by selling
generated by selling  units is governed by
units is governed by

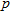 and the number of units for sale
and the number of units for sale  are related by the demand equation:
are related by the demand equation:
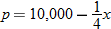
 of producing
of producing  items is governed by the equation
items is governed by the equation
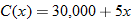
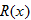 generated by selling
generated by selling  units is governed by
units is governed by
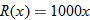
 the assembly line is running per day. The number of products manufactured
the assembly line is running per day. The number of products manufactured 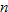 is a function of the number of hours
is a function of the number of hours  the assembly line is operating and is given by the function
the assembly line is operating and is given by the function 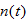 . The cost of manufacturing the product
. The cost of manufacturing the product 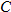 measured in thousands of dollars is a function of the quantity manufactured, that is, the function
measured in thousands of dollars is a function of the quantity manufactured, that is, the function 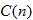 .
. the assembly line is running per day. The number of products manufactured
the assembly line is running per day. The number of products manufactured 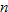 is a function of the number of hours
is a function of the number of hours  the assembly line is operating and is given by the function
the assembly line is operating and is given by the function 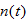 . The cost of manufacturing the product
. The cost of manufacturing the product 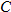 measured in thousands of dollars is a function of the quantity manufactured, that is, the function
measured in thousands of dollars is a function of the quantity manufactured, that is, the function 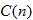 .
.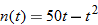
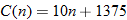
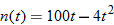
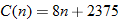
 measured in miles is a function of time
measured in miles is a function of time  measured in days from the start of the spill, while the area of the oil spill is a function of radius, that is, the function
measured in days from the start of the spill, while the area of the oil spill is a function of radius, that is, the function 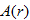 .
. measured in miles is a function of time
measured in miles is a function of time  measured in days from the start of the spill, while the area of the oil spill is a function of radius, that is, the function
measured in days from the start of the spill, while the area of the oil spill is a function of radius, that is, the function 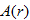 .
.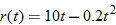
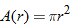
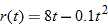
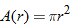
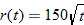 . Find the area of the spill as a function of time.
. Find the area of the spill as a function of time.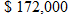 a few years ago, and when they list it with a realtor they will pay a
a few years ago, and when they list it with a realtor they will pay a 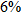 commission. Write a function that represents the amount of money they will make on their home as a function of the asking price
commission. Write a function that represents the amount of money they will make on their home as a function of the asking price 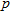 .
.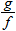
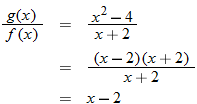
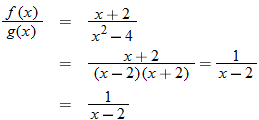

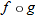
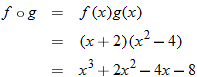
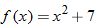 and
and 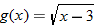 , find
, find 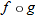 , and state the domain.
, and state the domain.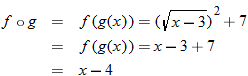
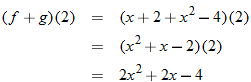
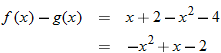
 and
and  ,
, 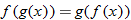 for all values of
for all values of  that are in the domain of both
that are in the domain of both  and
and  .
. and
and  ,
, 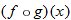 exists for all values of
exists for all values of  that are in the domain of
that are in the domain of  , provided the range of
, provided the range of  is a subset of the domain of
is a subset of the domain of  .
.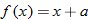 and
and 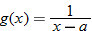 , find
, find 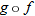 and state its domain.
and state its domain.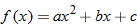 and
and 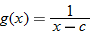 , find
, find 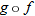 and state its domain.
and state its domain.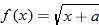 and
and 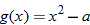 find
find 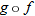 and state its domain.
and state its domain.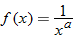 and
and 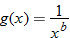 , find
, find 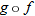 and state its domain. Assume
and state its domain. Assume 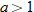 and
and 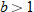 .
.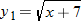 and
and 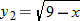 . Plot
. Plot 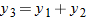 . What is the domain of
. What is the domain of 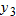 ?
?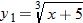 ,
, 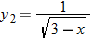 , and
, and 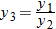 . What is the domain of
. What is the domain of 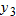 ?
?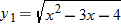 ,
, 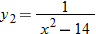 , and
, and 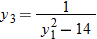 . If
. If 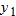 represents a function
represents a function  and
and 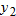 represents a function
represents a function  , then
, then 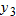 represents the composite function
represents the composite function 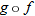 . The graph of
. The graph of 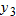 is only defined for the domain of
is only defined for the domain of 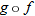 . State the domain of
. State the domain of 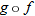 .
.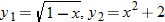 , and
, and 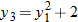 . If
. If 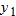 represents a function
represents a function  and
and 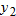 represents a function
represents a function  , then
, then 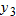 represents the composite function
represents the composite function 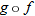 . The graph of
. The graph of 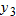 is only defined for the domain of
is only defined for the domain of 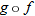 . State the domain of
. State the domain of 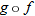 .
.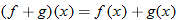
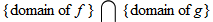
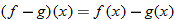
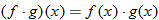
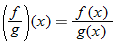

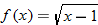 and
and 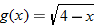 , determine the sum function, difference function, product function, and quotient function. State the domain of these four new functions.
, determine the sum function, difference function, product function, and quotient function. State the domain of these four new functions.

 �Technology Tip
�Technology Tip
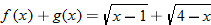
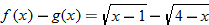
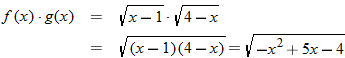
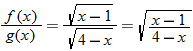
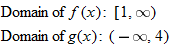
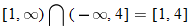
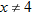 , so the domain of the quotient function is
, so the domain of the quotient function is 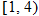 .
.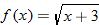 and
and 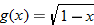 , find
, find 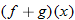 and state its domain.
and state its domain.
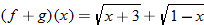
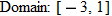
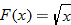 and
and 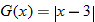 , find the quotient function,
, find the quotient function, 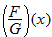 , and state its domain.
, and state its domain.
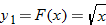 ,
, 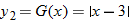 , and
, and 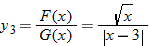 are shown.
are shown.
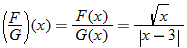
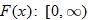
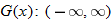
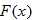 and the domain for
and the domain for 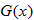 are represented by the intersection
are represented by the intersection 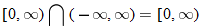 . Also, the denominator of the quotient function is equal to zero when
. Also, the denominator of the quotient function is equal to zero when 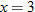 , so we must eliminate this value from the domain.
, so we must eliminate this value from the domain.
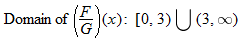
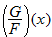 , and state its domain.
, and state its domain.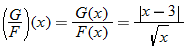


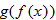

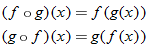
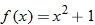 and
and  , find
, find 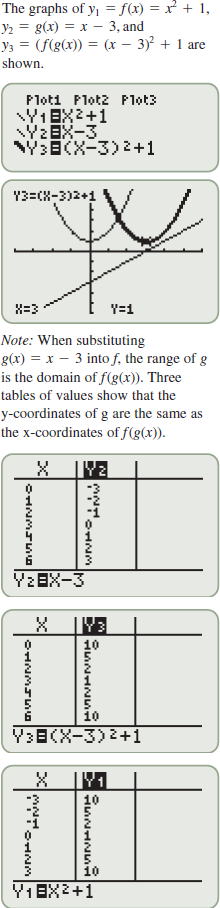
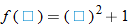
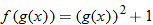
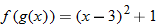
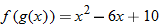
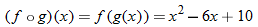
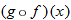 .
.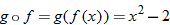
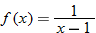 and
and 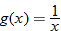 , determine
, determine 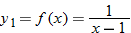 ,
, 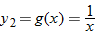 , and
, and 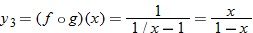 are shown.
are shown.

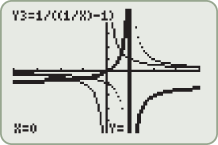
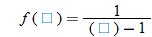
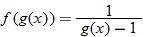
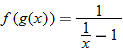
 .
.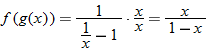
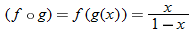
 . Therefore,
. Therefore, 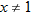 . Are there any other values for
. Are there any other values for 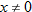 ; therefore we must also exclude zero.
; therefore we must also exclude zero. and
and 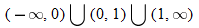
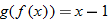 . Domain of
. Domain of 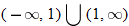 .
.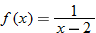 and
and 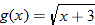 . Find the domain of
. Find the domain of 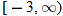
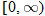
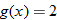 .
.
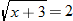
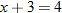
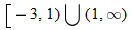
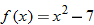 and
and 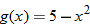 , evaluate:
, evaluate: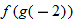
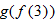
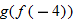
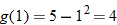
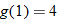 into
into 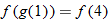
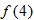 .
.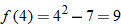
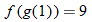
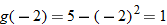
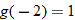 into
into 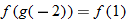
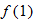 .
.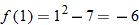
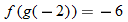
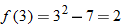
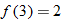 into
into 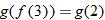
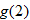 .
.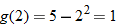
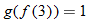
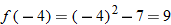
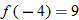 into
into 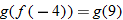
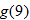 .
.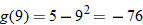
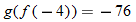
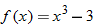 and
and 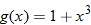 , evaluate
, evaluate 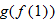 .
.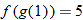 and
and 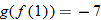
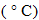 scale
scale
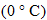 and boiling
and boiling 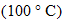 points of pure water at sea level into 100 equal parts. This scale is used in science and is one of the standards of the “metric” (SI) system of measurements.
points of pure water at sea level into 100 equal parts. This scale is used in science and is one of the standards of the “metric” (SI) system of measurements.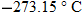 ), a hypothetical temperature at which there is a complete absence of heat energy.
), a hypothetical temperature at which there is a complete absence of heat energy.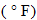 scale
scale
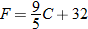
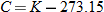 into the equation for
into the equation for 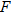 .
.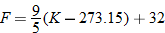
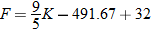
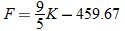
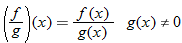
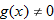 .
.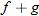 ,
, 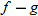 ,
, 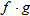 , and
, and 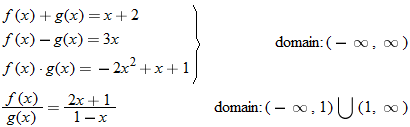

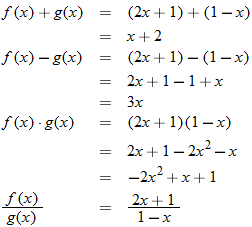
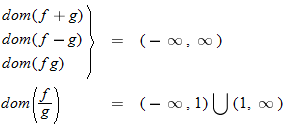
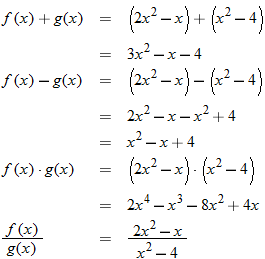
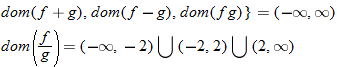
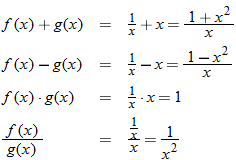
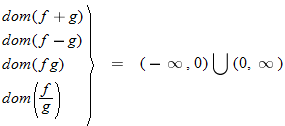
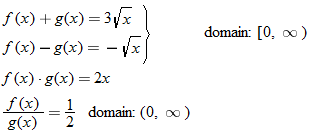
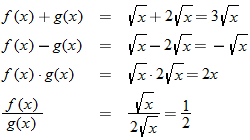
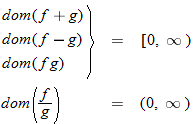
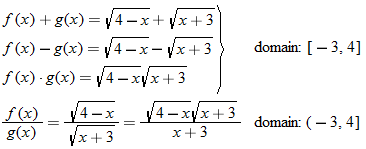
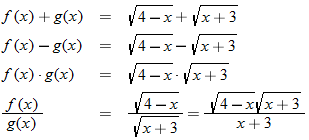
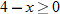 and
and 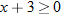 . So,
. So, 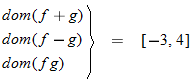 .
.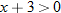 . So,
. So, 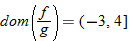 .
.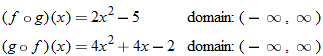
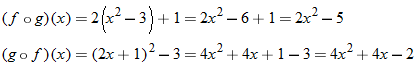

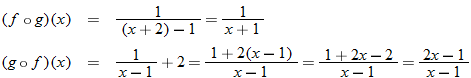
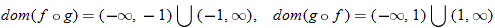
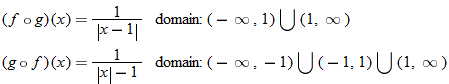
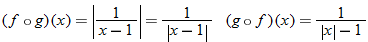
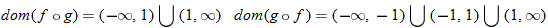
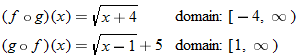
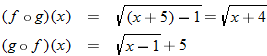
 : Must have
: Must have 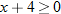 . So,
. So, 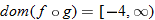 .
.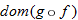 : Must have
: Must have 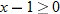 . So,
. So, 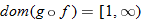 .
.
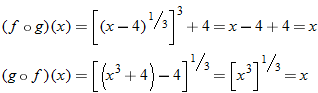
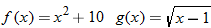
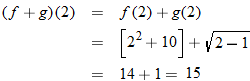
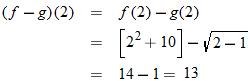
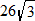
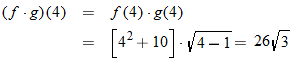
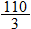
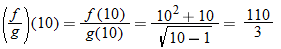
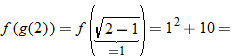
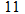
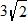
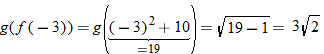
 is not defined. Hence,
is not defined. Hence, 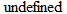 .
.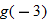 in not defined.
in not defined.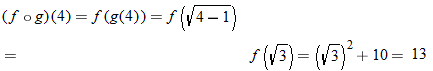
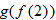 , if possible.
, if possible.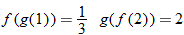
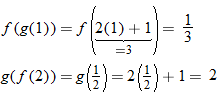
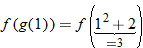 Since 3 is not in the domain of
Since 3 is not in the domain of 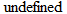 .
.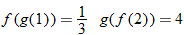
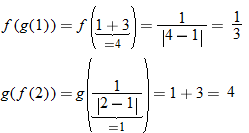
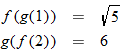
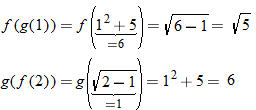
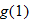 is not defined.
is not defined.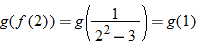 , which is not defined. So, this is also
, which is not defined. So, this is also 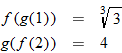
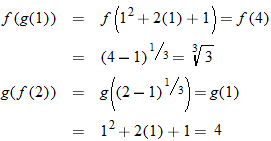
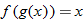 and
and 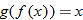 .
.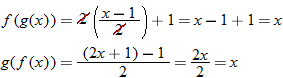
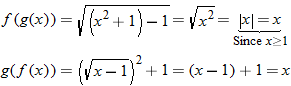
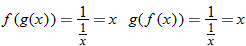
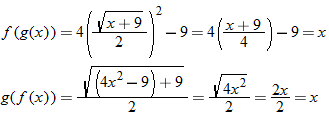
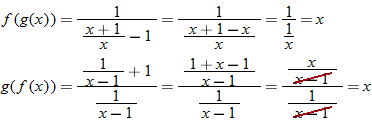
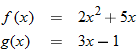
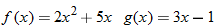
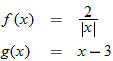
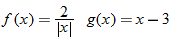
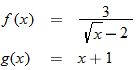
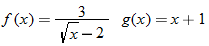
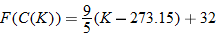
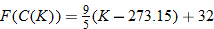
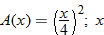 is the number of linear feet of fence.
is the number of linear feet of fence.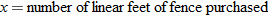 .
.
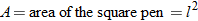 .
.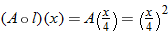 .
.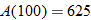 square feet.
square feet.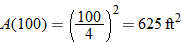
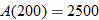 square feet.
square feet.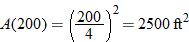
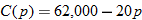
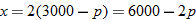
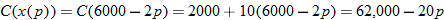
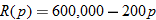
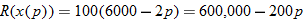
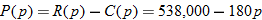
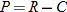 . So,
. So,
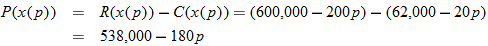
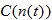 .
.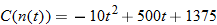
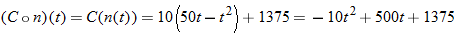
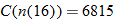
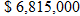 .
.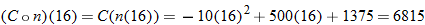
 .
.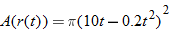
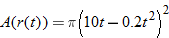
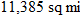
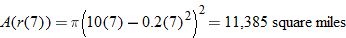
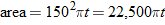
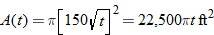
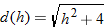
 .
.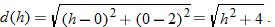

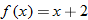 and
and 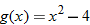 , find the indicated function and state its domain. Explain the mistake that is made in each problem.
, find the indicated function and state its domain. Explain the mistake that is made in each problem.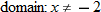
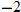 from the domain.
from the domain.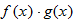
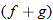 was multiplied by 2 when it ought to have been evaluated at 2.
was multiplied by 2 when it ought to have been evaluated at 2.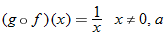
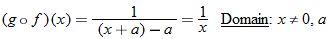
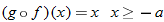
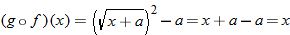
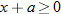 , so that
, so that 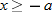 . So, domain is
. So, domain is 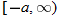 .
.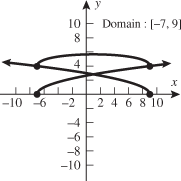
 .
. .
.
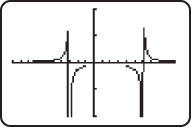
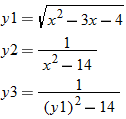
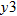 only is shown to the right.
only is shown to the right.