Horizontal and Vertical Shifts
The focus of the previous section was to learn the graphs that correspond to particular functions such as identity, square, cube, square root, cube root, absolute value, and reciprocal. Therefore, at this point, you should be able to recognize and generate the graphs of

, and

. In this section, we will discuss how to sketch the graphs of functions that are very simple modifications of these functions. For instance, a common function may be shifted (horizontally or vertically), reflected, or stretched (or compressed). Collectively, these techniques are called
transformations.
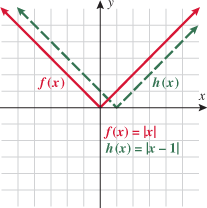
Let's take the absolute value function as an example. The graph of

was given in the last section. Now look at two examples that are much like this function:

and
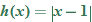
. Graphing these functions by point-plotting yields
Instead of point-plotting the function

, we could have started with the function

and shifted the entire graph
up 2 units. Similarly, we could have generated the graph of the function
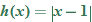
by shifting the function

to the
right 1 unit. In both cases, the base or starting function is

. Why did we go up for

and to the right for

?
Note that we could rewrite the functions

and

in terms of

:
In the case of

, the shift

occurs “outside” the function—that is, outside the parentheses showing the argument. Therefore, the output for

is two more than the typical output for

. Because the output corresponds to the vertical axis, this results in a shift
upward of two units. In general, shifts that occur
outside the function correspond to a
vertical shift corresponding to the sign of the shift. For instance, had the function been

, this graph would have started with the graph of the function

and shifted down two units.
In the case of

, the shift occurs “inside” the function—that is, inside the parentheses showing the argument. Note that the point

that lies on the graph of

was shifted to the point
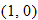
on the graph of the function

. The

remained the same, but the
shifted to the right one unit. Similarly, the points

and
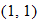
were shifted to the points

and

, respectively. In general, shifts that occur
inside the function correspond to a
horizontal shift opposite the sign. In this case, the graph of the function

shifted the graph of the function

to the right one unit. If, instead, we had the function

, this graph would have started with the graph of the function

and shifted to the left one unit.
Assuming that  is a positive constant,
To Graph |
Shift the Graph of 
|
|
 units upward |
|
 units downward |
|
|
Adding or subtracting a constant outside the function corresponds to a vertical shift that goes with the sign. |
|
|
 |
Shifts outside the function are vertical shifts with the sign.
|
|
|
|
|
Assuming that  is a positive constant,
To Graph |
Shift the Graph of 
|
|
 units to the left |
|
 units to the right |
|
|
Adding or subtracting a constant inside the function corresponds to a horizontal shift that goes opposite the sign. |
|
|
 |
Shifts inside the function are horizontal shifts opposite the sign.
|
|
|
|
|
|
EXAMPLE�1�
|
Horizontal and Vertical Shifts |
|
Sketch the graphs of the given functions using horizontal and vertical shifts:
 |
 �Technology Tip� �Technology Tip� |
|
|
|
|
|
Solution
In both cases, the function to start with is  .
|
|
Sketch the graphs of the given functions using horizontal and vertical shifts.
|
|
|
|
|
|
It is important to note that the domain and range of the resulting function can be thought of as also being shifted. Shifts in the domain correspond to horizontal shifts, and shifts in the range correspond to vertical shifts.
 �EXAMPLE�2� �EXAMPLE�2�
|
Horizontal and Vertical Shifts and Changes in the Domain and Range |
|
Graph the functions using translations and state the domain and range of each function.
Solution
In both cases the function to start with is  . |
|
|
|
|
The original function  has an implicit restriction on the domain:  . The function  also has the implicit restriction that 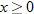 . The output or range of 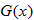 is always two units less than the output of the original function  .
|
|
Sketch the graph of the functions using shifts and state the domain and range.
|
|
|
|
|
|
The previous examples have involved graphing functions by shifting a known function either in the horizontal or vertical direction. Let us now look at combinations of horizontal and vertical shifts.
 �EXAMPLE�3� �EXAMPLE�3�
|
Combining Horizontal and Vertical Shifts |
|
Sketch the graph of the function  . State the domain and range of 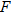 .
 |
 �Technology Tip� �Technology Tip� |
|
|
|
|
|
Solution
The base function is  .
|
|
Sketch the graph of the function  . State the domain and range of  .
|
|
|
|
|
|
All of the previous transformation examples involve starting with a common function and shifting the function in either the horizontal or the vertical direction (or a combination of both). Now, let's investigate
reflections of functions about the

or
.
Reflection about the Axes
To sketch the graphs of

and

start by first listing points that are on each of the graphs and then connecting the points with smooth curves.
Note that if the graph of

is reflected about the

, the result is the graph of

. Also note that the function

can be written as the negative of the function

; that is,

. In general,
reflection about the 
is produced by multiplying a function by
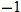
.
Let's now investigate reflection about the
. To sketch the graphs of

and

start by listing points that are on each of the graphs and then connecting the points with smooth curves.
Note that if the graph of

is reflected about the
, the result is the graph of

. Also note that the function

can be written as

. In general,
reflection about the 
is produced by replacing

with

in the function. Notice that the domain of

is
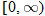
, whereas the domain of

is

.
REFLECTION ABOUT THE AXES |
|
|
The graph of  is obtained by reflecting the graph of  about the  . The graph of  is obtained by reflecting the graph of  about the  . |
|
|
|
EXAMPLE�4�
|
Sketching the Graph of a Function Using Both Shifts and Reflections |
|
Sketch the graph of the function  .
Solution
Start with the square root function. |
|
Shift the graph of  to the left one unit to arrive at the graph of 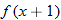 . |
|
Reflect the graph of 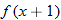 about the  to arrive at the graph of  . |
|
| � |
|
|
|
|
|
|
|
 �EXAMPLE�5� �EXAMPLE�5�
|
Sketching the Graph of a Function Using Both Shifts and Reflections |
|
Sketch the graph of the function  .
 |
 �Technology Tip� �Technology Tip� |
|
|
|
|
|
Solution
Start with the square root function. |
|
Shift the graph of  to the left two units to arrive at the graph of  . |
|
Reflect the graph of  about the 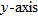 to arrive at the graph of  . |
|
Shift the graph  up one unit to arrive at the graph of  . |
|
| � |
|
|
|
|
|
Use shifts and reflections to sketch the graph of the function  . State the domain and range of  .
|
|
|
|
|
|
Look back at the order in which transformations were performed in Example
5: horizontal shift, reflection, and then vertical shift. Let us consider an alternate order of transformations.
Words |
Math |
Start with the square root function. |
|
Shift the graph of  up one unit to arrive at the graph of  . |
|
Reflect the graph of  about the 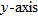 to arrive at the graph of  . |
|
Replace  with  , which corresponds to a shift of the graph of  to the right two units to arrive at the graph of  . |
|
In the last step we replaced  with  , which required us to think ahead knowing the desired result was  inside the radical. To avoid any possible confusion, follow this order of transformations:
|
|
|
|
Stretching and Compressing
Horizontal shifts, vertical shifts, and reflections change only the position of the graph in the Cartesian plane, leaving the basic shape of the graph unchanged. These transformations (shifts and reflections) are called rigid transformations because they alter only the position. Nonrigid transformations, on the other hand, distort the shape of the original graph. We now consider stretching and compressing of graphs in both the vertical and the horizontal direction.
A vertical stretch or compression of a graph occurs when the function is multiplied by a positive constant. For example, the graphs of the functions

,

, and

are illustrated below. Depending on if the constant is larger than 1 or smaller than 1 will determine whether it corresponds to a stretch (expansion) or compression (contraction) in the vertical direction.
Note that when the function

is multiplied by 2, so that

, the result is a graph stretched in the vertical direction. When the function

is multiplied by

, so that

, the result is a graph that is compressed in the vertical direction.
VERTICAL STRETCHING AND VERTICAL COMPRESSING OF GRAPHS |
|
|
The graph of  is found by:
 |
|
■�� |
Vertically stretching the graph of 
|
|
|
if 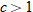
|
 |
|
■�� |
Vertically compressing the graph of 
|
|
|
if 
|
|
|
 is any positive real number. |
|
|
|
EXAMPLE�6�
|
Vertically Stretching and Compressing Graphs |
|
Graph the function  .
Solution
1. Start with the cube function. |
|
2. Vertical compression is expected because  is less than 1. |
|
3. Determine a few points that lie on the graph of  .
|
|
|
|
|
|
|
|
Conversely, if the argument

of a function

is multiplied by a positive real number

, then the result is a
horizontal stretch of the graph of

if

. If
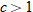
, then the result is a
horizontal compression of the graph of

.
HORIZONTAL STRETCHING AND HORIZONTAL COMPRESSING OF GRAPHS |
|
|
The graph of  is found by:
Note:  is any positive real number. |
|
|
 �EXAMPLE�7� �EXAMPLE�7�
|
Vertically Stretching and Horizontally Compressing Graphs |
|
Given the graph of  , graph:
|
|
Graph the function  .
Stretching of the graph  .
|
|
|
|
|
|
 �EXAMPLE�8� �EXAMPLE�8�
|
Sketching the Graph of a Function Using Multiple Transformations |
|
Sketch the graph of the function  .
 |
 �Technology Tip� �Technology Tip� |
|
|
Graphs of  ,  , and  are shown.
|
|
|
|
|
Solution
Start with the square function. |
|
Shift the graph of  to the right three units to arrive at the graph of  . |
|
Vertically stretch the graph of  by a factor of 2 to arrive at the graph of  . |
|
Reflect the graph  about the  to arrive at the graph of  . |
|
|
|
|
|
|
|
|
In Example
8 we followed the same “inside out” approach with the functions to determine the order for the transformations: horizontal shift, vertical stretch, and reflection.
 �
� , and
, and  . In this section, we will discuss how to sketch the graphs of functions that are very simple modifications of these functions. For instance, a common function may be shifted (horizontally or vertically), reflected, or stretched (or compressed). Collectively, these techniques are called transformations.
. In this section, we will discuss how to sketch the graphs of functions that are very simple modifications of these functions. For instance, a common function may be shifted (horizontally or vertically), reflected, or stretched (or compressed). Collectively, these techniques are called transformations. , and
, and  . In this section, we will discuss how to sketch the graphs of functions that are very simple modifications of these functions. For instance, a common function may be shifted (horizontally or vertically), reflected, or stretched (or compressed). Collectively, these techniques are called transformations.
. In this section, we will discuss how to sketch the graphs of functions that are very simple modifications of these functions. For instance, a common function may be shifted (horizontally or vertically), reflected, or stretched (or compressed). Collectively, these techniques are called transformations. was given in the last section. Now look at two examples that are much like this function:
was given in the last section. Now look at two examples that are much like this function:  and
and 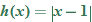 . Graphing these functions by point-plotting yields
. Graphing these functions by point-plotting yields
 was given in the last section. Now look at two examples that are much like this function:
was given in the last section. Now look at two examples that are much like this function:  and
and 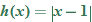 . Graphing these functions by point-plotting yields
. Graphing these functions by point-plotting yields
 , we could have started with the function
, we could have started with the function  and shifted the entire graph up 2 units. Similarly, we could have generated the graph of the function
and shifted the entire graph up 2 units. Similarly, we could have generated the graph of the function 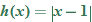 by shifting the function
by shifting the function  to the right 1 unit. In both cases, the base or starting function is
to the right 1 unit. In both cases, the base or starting function is  . Why did we go up for
. Why did we go up for  and to the right for
and to the right for  ?
? , we could have started with the function
, we could have started with the function  and shifted the entire graph up 2 units. Similarly, we could have generated the graph of the function
and shifted the entire graph up 2 units. Similarly, we could have generated the graph of the function 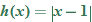 by shifting the function
by shifting the function  to the right 1 unit. In both cases, the base or starting function is
to the right 1 unit. In both cases, the base or starting function is  . Why did we go up for
. Why did we go up for  and to the right for
and to the right for  ?
? and
and  in terms of
in terms of  :
:

 and
and  in terms of
in terms of  :
:

 , the shift
, the shift  occurs “outside” the function—that is, outside the parentheses showing the argument. Therefore, the output for
occurs “outside” the function—that is, outside the parentheses showing the argument. Therefore, the output for  is two more than the typical output for
is two more than the typical output for  . Because the output corresponds to the vertical axis, this results in a shift upward of two units. In general, shifts that occur outside the function correspond to a vertical shift corresponding to the sign of the shift. For instance, had the function been
. Because the output corresponds to the vertical axis, this results in a shift upward of two units. In general, shifts that occur outside the function correspond to a vertical shift corresponding to the sign of the shift. For instance, had the function been  , this graph would have started with the graph of the function
, this graph would have started with the graph of the function  and shifted down two units.
and shifted down two units. , the shift
, the shift  occurs “outside” the function—that is, outside the parentheses showing the argument. Therefore, the output for
occurs “outside” the function—that is, outside the parentheses showing the argument. Therefore, the output for  is two more than the typical output for
is two more than the typical output for  . Because the output corresponds to the vertical axis, this results in a shift upward of two units. In general, shifts that occur outside the function correspond to a vertical shift corresponding to the sign of the shift. For instance, had the function been
. Because the output corresponds to the vertical axis, this results in a shift upward of two units. In general, shifts that occur outside the function correspond to a vertical shift corresponding to the sign of the shift. For instance, had the function been  , this graph would have started with the graph of the function
, this graph would have started with the graph of the function  and shifted down two units.
and shifted down two units. , the shift occurs “inside” the function—that is, inside the parentheses showing the argument. Note that the point
, the shift occurs “inside” the function—that is, inside the parentheses showing the argument. Note that the point  that lies on the graph of
that lies on the graph of  was shifted to the point
was shifted to the point 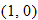 on the graph of the function
on the graph of the function  . The
. The  remained the same, but the
remained the same, but the  shifted to the right one unit. Similarly, the points
shifted to the right one unit. Similarly, the points  and
and 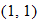 were shifted to the points
were shifted to the points  and
and  , respectively. In general, shifts that occur inside the function correspond to a horizontal shift opposite the sign. In this case, the graph of the function
, respectively. In general, shifts that occur inside the function correspond to a horizontal shift opposite the sign. In this case, the graph of the function  shifted the graph of the function
shifted the graph of the function  to the right one unit. If, instead, we had the function
to the right one unit. If, instead, we had the function  , this graph would have started with the graph of the function
, this graph would have started with the graph of the function  and shifted to the left one unit.
and shifted to the left one unit.
 , the shift occurs “inside” the function—that is, inside the parentheses showing the argument. Note that the point
, the shift occurs “inside” the function—that is, inside the parentheses showing the argument. Note that the point  that lies on the graph of
that lies on the graph of  was shifted to the point
was shifted to the point 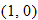 on the graph of the function
on the graph of the function  . The
. The  remained the same, but the
remained the same, but the 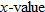 shifted to the right one unit. Similarly, the points
shifted to the right one unit. Similarly, the points  and
and 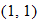 were shifted to the points
were shifted to the points  and
and  , respectively. In general, shifts that occur inside the function correspond to a horizontal shift opposite the sign. In this case, the graph of the function
, respectively. In general, shifts that occur inside the function correspond to a horizontal shift opposite the sign. In this case, the graph of the function  shifted the graph of the function
shifted the graph of the function  to the right one unit. If, instead, we had the function
to the right one unit. If, instead, we had the function  , this graph would have started with the graph of the function
, this graph would have started with the graph of the function  and shifted to the left one unit.
and shifted to the left one unit.
 or
or  .
. or
or  .
. and
and  start by first listing points that are on each of the graphs and then connecting the points with smooth curves.
start by first listing points that are on each of the graphs and then connecting the points with smooth curves.
 is reflected about the
is reflected about the  , the result is the graph of
, the result is the graph of  . Also note that the function
. Also note that the function  can be written as the negative of the function
can be written as the negative of the function  ; that is,
; that is,  . In general, reflection about the
. In general, reflection about the  is produced by multiplying a function by
is produced by multiplying a function by 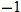 .
. and
and  start by first listing points that are on each of the graphs and then connecting the points with smooth curves.
start by first listing points that are on each of the graphs and then connecting the points with smooth curves.
 is reflected about the
is reflected about the  , the result is the graph of
, the result is the graph of  . Also note that the function
. Also note that the function  can be written as the negative of the function
can be written as the negative of the function  ; that is,
; that is,  . In general, reflection about the
. In general, reflection about the  is produced by multiplying a function by
is produced by multiplying a function by 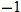 .
. . To sketch the graphs of
. To sketch the graphs of  and
and  start by listing points that are on each of the graphs and then connecting the points with smooth curves.
start by listing points that are on each of the graphs and then connecting the points with smooth curves.
 is reflected about the
is reflected about the  , the result is the graph of
, the result is the graph of  . Also note that the function
. Also note that the function  can be written as
can be written as  . In general, reflection about the
. In general, reflection about the  is produced by replacing
is produced by replacing  with
with  in the function. Notice that the domain of
in the function. Notice that the domain of  is
is 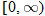 , whereas the domain of
, whereas the domain of  is
is  .
. . To sketch the graphs of
. To sketch the graphs of  and
and  start by listing points that are on each of the graphs and then connecting the points with smooth curves.
start by listing points that are on each of the graphs and then connecting the points with smooth curves.
 is reflected about the
is reflected about the  , the result is the graph of
, the result is the graph of  . Also note that the function
. Also note that the function  can be written as
can be written as  . In general, reflection about the
. In general, reflection about the  is produced by replacing
is produced by replacing  with
with  in the function. Notice that the domain of
in the function. Notice that the domain of  is
is 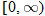 , whereas the domain of
, whereas the domain of  is
is  .
. ,
,  , and
, and  are illustrated below. Depending on if the constant is larger than 1 or smaller than 1 will determine whether it corresponds to a stretch (expansion) or compression (contraction) in the vertical direction.
are illustrated below. Depending on if the constant is larger than 1 or smaller than 1 will determine whether it corresponds to a stretch (expansion) or compression (contraction) in the vertical direction.
 is multiplied by 2, so that
is multiplied by 2, so that  , the result is a graph stretched in the vertical direction. When the function
, the result is a graph stretched in the vertical direction. When the function  is multiplied by
is multiplied by  , so that
, so that  , the result is a graph that is compressed in the vertical direction.
, the result is a graph that is compressed in the vertical direction.
 ,
,  , and
, and  are illustrated below. Depending on if the constant is larger than 1 or smaller than 1 will determine whether it corresponds to a stretch (expansion) or compression (contraction) in the vertical direction.
are illustrated below. Depending on if the constant is larger than 1 or smaller than 1 will determine whether it corresponds to a stretch (expansion) or compression (contraction) in the vertical direction.
 is multiplied by 2, so that
is multiplied by 2, so that  , the result is a graph stretched in the vertical direction. When the function
, the result is a graph stretched in the vertical direction. When the function  is multiplied by
is multiplied by  , so that
, so that  , the result is a graph that is compressed in the vertical direction.
, the result is a graph that is compressed in the vertical direction.
 of a function
of a function  is multiplied by a positive real number
is multiplied by a positive real number  , then the result is a horizontal stretch of the graph of
, then the result is a horizontal stretch of the graph of  if
if  . If
. If 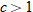 , then the result is a horizontal compression of the graph of
, then the result is a horizontal compression of the graph of  .
.
 of a function
of a function  is multiplied by a positive real number
is multiplied by a positive real number  , then the result is a horizontal stretch of the graph of
, then the result is a horizontal stretch of the graph of  if
if  . If
. If 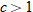 , then the result is a horizontal compression of the graph of
, then the result is a horizontal compression of the graph of  .
.
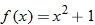













 and the
and the 
















































 per hour. Write the function that describes the current salary of the employee as a function of the number of hours worked per week,
per hour. Write the function that describes the current salary of the employee as a function of the number of hours worked per week,  . After a year, the manager decides to award the employee a raise equivalent to paying him for an additional 5 hours per week. Write a function that describes the salary of the employee after the raise.
. After a year, the manager decides to award the employee a raise equivalent to paying him for an additional 5 hours per week. Write a function that describes the salary of the employee after the raise. , where
, where  is the number of pallets sold per year in a normal year. In rainy years Sod King gives away 10 free pallets per year. Write the function that describes the profit of
is the number of pallets sold per year in a normal year. In rainy years Sod King gives away 10 free pallets per year. Write the function that describes the profit of  pallets of sod in rainy years.
pallets of sod in rainy years. . That year the standard deduction was
. That year the standard deduction was  and her tax bracket paid
and her tax bracket paid  in taxes. Write the function that will determine her 2012 taxes, assuming she receives the raise that places her in the
in taxes. Write the function that will determine her 2012 taxes, assuming she receives the raise that places her in the  bracket.
bracket. is given by
is given by  , where
, where  is the weight of the infant in ounces. In emergencies there is often not enough time to weigh the infant, so nurses have to estimate the baby's weight. What is the function that represents the actual amount of medication the infant is given if his weight is overestimated by 3 ounces?
is the weight of the infant in ounces. In emergencies there is often not enough time to weigh the infant, so nurses have to estimate the baby's weight. What is the function that represents the actual amount of medication the infant is given if his weight is overestimated by 3 ounces? where
where  is weight in kilograms and
is weight in kilograms and  is height in centimeters. Since BSA depends on weight and height, it is often thought of as a function of both weight and height. However, for an individual adult height is generally considered constant; thus BSA can be thought of as a function of weight alone.
is height in centimeters. Since BSA depends on weight and height, it is often thought of as a function of both weight and height. However, for an individual adult height is generally considered constant; thus BSA can be thought of as a function of weight alone.
 is weight in kilograms and
is weight in kilograms and  is height in centimeters. Since BSA depends on weight and height, it is often thought of as a function of both weight and height. However, for an individual adult height is generally considered constant; thus BSA can be thought of as a function of weight alone.
is height in centimeters. Since BSA depends on weight and height, it is often thought of as a function of both weight and height. However, for an individual adult height is generally considered constant; thus BSA can be thought of as a function of weight alone. .
. .
. .
. .
. is the same as the graph of
is the same as the graph of  .
. is the same as the graph of
is the same as the graph of  .
. and then the
and then the  , the result is the graph of the original odd function.
, the result is the graph of the original odd function. is reflected about the
is reflected about the  , it produces the same graph as if it had been reflected about the
, it produces the same graph as if it had been reflected about the  .
. lies on the graph of the function
lies on the graph of the function  . What point is guaranteed to lie on the graph of
. What point is guaranteed to lie on the graph of  ?
? lies on the graph of the function
lies on the graph of the function  . What point is guaranteed to lie on the graph of
. What point is guaranteed to lie on the graph of  ?
? and
and  ?
? and
and  ?
? and
and  , assuming that
, assuming that  is positive?
is positive? and
and  , assuming that
, assuming that  is positive?
is positive? . Use transforms to describe the relationship between
. Use transforms to describe the relationship between  and
and  .
. . Use transforms to describe the relationship between
. Use transforms to describe the relationship between  and
and  .
.

































 �Technology Tip�
�Technology Tip� and
and  are shown.
are shown.


 are shown.
are shown.





 can be rewritten as
can be rewritten as  .
.

 can be rewritten as
can be rewritten as  .
.










 can be rewritten as
can be rewritten as  .
.
 , which lies on the graph of
, which lies on the graph of  on the graph of
on the graph of 
 , the function
, the function  . We see that the output or range of
. We see that the output or range of 
 can be rewritten as
can be rewritten as  .
.
 on the graph of
on the graph of  .
.
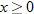 . The output or range of
. The output or range of 






 . State the domain and range of
. State the domain and range of 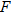 .
.
 , and
, and  are shown.
are shown.


 .
.
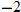 shift is
shift is  on the graph of
on the graph of  .
.

 . State the domain and range of
. State the domain and range of 









 is obtained by reflecting the graph of
is obtained by reflecting the graph of  .
. is obtained by reflecting the graph of
is obtained by reflecting the graph of  .
. .
.
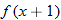 .
.
 .
.

 .
.
 ,
,  ,
,  , and
, and  are shown.
are shown.



 .
.
 .
.
 .
.

 . State the domain and range of
. State the domain and range of 

 .
.
 .
.
 , which corresponds to a shift of the graph of
, which corresponds to a shift of the graph of  .
. inside the radical. To avoid any possible confusion, follow this order of transformations:
inside the radical. To avoid any possible confusion, follow this order of transformations:

 and/or
and/or 








 is found by:
is found by:
 .
.
 is less than 1.
is less than 1.
 .
.


 is found by:
is found by:





 of
of 
 of
of 
 .
.
 .
.
 ,
,  , and
, and  are shown.
are shown.



 .
.
 .
.
 .
.

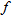
 .
. .
. .
. .
.












 up 1 unit.
up 1 unit. right 1 unit, then shift up 1 unit.
right 1 unit, then shift up 1 unit. , and then shift down 1 unit.
, and then shift down 1 unit.


 (since
(since  )
)

 , but is transformed accordingly.
, but is transformed accordingly.






































































 over
over 









 right 1 unit, then up 2 units.
right 1 unit, then up 2 units.


 left 3 units, then up 2 units.
left 3 units, then up 2 units.





 , where
, where  , and
, and 








 and
and 
 . Then, the salary is given by
. Then, the salary is given by  (in dollars). After 1 year, taking into account the raise, the new salary is
(in dollars). After 1 year, taking into account the raise, the new salary is  .
.


 to get
to get  .
. .
.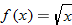 .
. .
. ; therefore, shift to the
; therefore, shift to the  . The correct sequence of steps would be:
. The correct sequence of steps would be:  , where
, where  : Shift to the right 3
: Shift to the right 3 .
.
 is the graph of
is the graph of  is on the graph of the translation
is on the graph of the translation 
 and
and 
 that is below the
that is below the  .
.

 .
.
 and
and 


 , you have a horizontal stretch. If
, you have a horizontal stretch. If  , the graph is a horizontal compression.
, the graph is a horizontal compression.

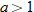 , then the graph is a horizontal compression.
, then the graph is a horizontal compression. , then the graph is a horizontal expansion.
, then the graph is a horizontal expansion.

 is stretched twice in length. There is a vertical shift of one unit up.
is stretched twice in length. There is a vertical shift of one unit up.
 is stretched by a factor of 2. Any portion of the graph that is below the
is stretched by a factor of 2. Any portion of the graph that is below the