|
SECTION 3.2 |
Graphs of Functions; Piecewise-Defined Functions; Increasing and Decreasing Functions; Average Rate of Change |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
 �
�Recognizing and Classifying Functions
3.2.1.1�Common Functions
Point-plotting techniques were introduced in Section 2.2, and we noted there that we would explore some more efficient ways of graphing functions in Chapter 3. The nine main functions you will read about in this section will constitute a “library” of functions that you should commit to memory. We will draw on this library of functions in the next section when graphing transformations are discussed. Several of these functions have been shown previously in this chapter, but now we will classify them specifically by name and identify properties that each function exhibits.
In Section 2.3, we discussed equations and graphs of lines. All lines (with the exception of vertical lines) pass the vertical line test, and hence are classified as functions. Instead of the traditional notation of a line, 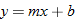 , we use function notation and classify a function whose graph is a line as a linear function.
, we use function notation and classify a function whose graph is a line as a linear function.
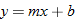 , we use function notation and classify a function whose graph is a line as a linear function.
, we use function notation and classify a function whose graph is a line as a linear function.
|
The domain of a linear function 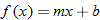 is the set of all real numbers
is the set of all real numbers  . The graph of this function has slope
. The graph of this function has slope 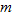 and
and 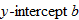 .
.
One special case of the linear function is the constant function 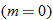 .
.
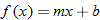 is the set of all real numbers
is the set of all real numbers 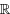 . The graph of this function has slope
. The graph of this function has slope 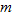 and
and 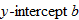 .
.
|
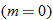 .
.
|
The graph of a constant function 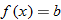 is a horizontal line. The
is a horizontal line. The  corresponds to the point
corresponds to the point 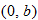 . The domain of a constant function is the set of all real numbers
. The domain of a constant function is the set of all real numbers 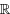 . The range, however, is a single value
. The range, however, is a single value 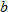 . In other words, all
. In other words, all 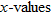 correspond to a single
correspond to a single 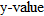 .
.
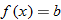 is a horizontal line. The
is a horizontal line. The  corresponds to the point
corresponds to the point 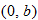 . The domain of a constant function is the set of all real numbers
. The domain of a constant function is the set of all real numbers 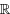 . The range, however, is a single value
. The range, however, is a single value 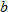 . In other words, all
. In other words, all  correspond to a single
correspond to a single  .
.
|
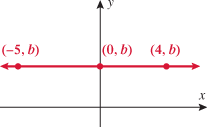
Another specific example of a linear function is the function having a slope of one 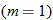 and a
and a  of zero
of zero 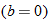 . This special case is called the identity function.
. This special case is called the identity function.
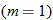 and a
and a  of zero
of zero 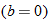 . This special case is called the identity function.
. This special case is called the identity function.
|
The graph of the identity function has the following properties: It passes through the origin, and every point that lies on the line has equal 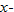 and
and 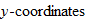 . Both the domain and the range of the identity function are the set of all real numbers
. Both the domain and the range of the identity function are the set of all real numbers 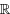 .
.
 and
and 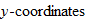 . Both the domain and the range of the identity function are the set of all real numbers
. Both the domain and the range of the identity function are the set of all real numbers 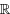 .
.
|
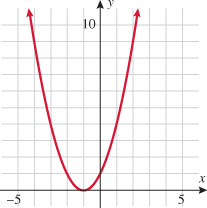
A function that squares the input is called the square function.
The graph of the square function is called a parabola and will be discussed in further detail in Chapters 4 and 8. The domain of the square function is the set of all real numbers 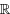 . Because squaring a real number always yields a positive number or zero, the range of the square function is the set of all nonnegative numbers. Note that the intercept is the origin and the square function is symmetric about the
. Because squaring a real number always yields a positive number or zero, the range of the square function is the set of all nonnegative numbers. Note that the intercept is the origin and the square function is symmetric about the  . This graph is contained in quadrants I and II.
. This graph is contained in quadrants I and II.
|
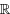 . Because squaring a real number always yields a positive number or zero, the range of the square function is the set of all nonnegative numbers. Note that the intercept is the origin and the square function is symmetric about the
. Because squaring a real number always yields a positive number or zero, the range of the square function is the set of all nonnegative numbers. Note that the intercept is the origin and the square function is symmetric about the  . This graph is contained in quadrants I and II.
. This graph is contained in quadrants I and II.
|
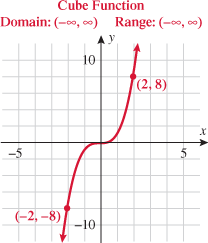
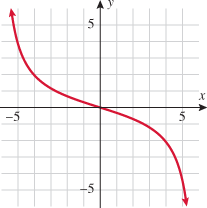
A function that cubes the input is called the cube function.
The domain of the cube function is the set of all real numbers 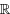 . Because cubing a negative number yields a negative number, cubing a positive number yields a positive number, and cubing 0 yields 0, the range of the cube function is also the set of all real numbers
. Because cubing a negative number yields a negative number, cubing a positive number yields a positive number, and cubing 0 yields 0, the range of the cube function is also the set of all real numbers 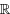 . Note that the only intercept is the origin and the cube function is symmetric about the origin. This graph extends only into quadrants I and III.
. Note that the only intercept is the origin and the cube function is symmetric about the origin. This graph extends only into quadrants I and III.
|
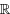 . Because cubing a negative number yields a negative number, cubing a positive number yields a positive number, and cubing 0 yields 0, the range of the cube function is also the set of all real numbers
. Because cubing a negative number yields a negative number, cubing a positive number yields a positive number, and cubing 0 yields 0, the range of the cube function is also the set of all real numbers 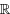 . Note that the only intercept is the origin and the cube function is symmetric about the origin. This graph extends only into quadrants I and III.
. Note that the only intercept is the origin and the cube function is symmetric about the origin. This graph extends only into quadrants I and III.
|
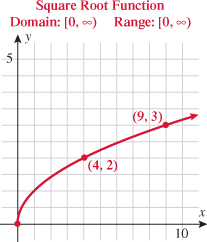
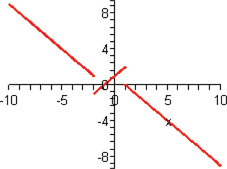
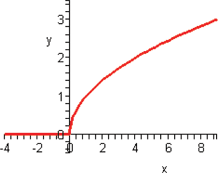
The next two functions are counterparts of the previous two functions: square root and cube root. When a function takes the square root of the input or the cube root of the input, the function is called the square root function or the cube root function, respectively.
In Section 3.1, we found the domain to be 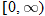 . The output of the function will be all real numbers greater than or equal to zero. Therefore, the range of the square root function is
. The output of the function will be all real numbers greater than or equal to zero. Therefore, the range of the square root function is 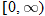 . The graph of this function will be contained in quadrant I.
. The graph of this function will be contained in quadrant I.
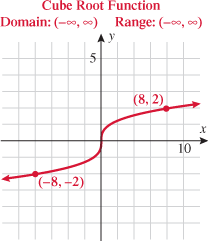
In Section 3.1, we stated the domain of the cube root function to be 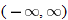 . We see by the graph that the range is also
. We see by the graph that the range is also 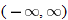 . This graph is contained in quadrants I and III and passes through the origin. This function is symmetric about the origin.
. This graph is contained in quadrants I and III and passes through the origin. This function is symmetric about the origin.
|
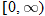 . The output of the function will be all real numbers greater than or equal to zero. Therefore, the range of the square root function is
. The output of the function will be all real numbers greater than or equal to zero. Therefore, the range of the square root function is 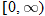 . The graph of this function will be contained in quadrant I.
. The graph of this function will be contained in quadrant I.
|
|
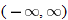 . We see by the graph that the range is also
. We see by the graph that the range is also 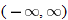 . This graph is contained in quadrants I and III and passes through the origin. This function is symmetric about the origin.
. This graph is contained in quadrants I and III and passes through the origin. This function is symmetric about the origin.
|
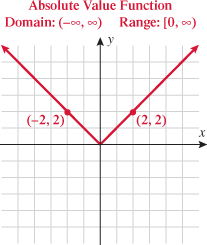
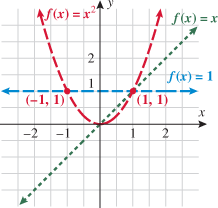
In Section 1.7, you read about absolute value equations and inequalities. Now we shift our focus to the graph of the absolute value function.
Some points that are on the graph of the absolute value function are 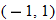 ,
, 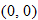 , and
, and 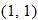 . The domain of the absolute value function is the set of all real numbers
. The domain of the absolute value function is the set of all real numbers 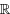 , yet the range is the set of nonnegative real numbers. The graph of this function is symmetric with respect to the
, yet the range is the set of nonnegative real numbers. The graph of this function is symmetric with respect to the  and is contained in quadrants I and II.
and is contained in quadrants I and II.
|
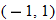 ,
, 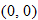 , and
, and 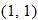 . The domain of the absolute value function is the set of all real numbers
. The domain of the absolute value function is the set of all real numbers 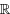 , yet the range is the set of nonnegative real numbers. The graph of this function is symmetric with respect to the
, yet the range is the set of nonnegative real numbers. The graph of this function is symmetric with respect to the 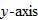 and is contained in quadrants I and II.
and is contained in quadrants I and II.
|
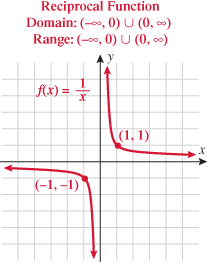
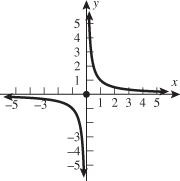
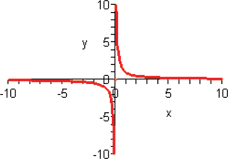
A function whose output is the reciprocal of its input is called the reciprocal function.
The only restriction on the domain of the reciprocal function is that 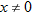 . Therefore, we say the domain is the set of all real numbers excluding zero. The graph of the reciprocal function illustrates that its range is also the set of all real numbers except zero. Note that the reciprocal function is symmetric with respect to the origin and is contained in quadrants I and III.
. Therefore, we say the domain is the set of all real numbers excluding zero. The graph of the reciprocal function illustrates that its range is also the set of all real numbers except zero. Note that the reciprocal function is symmetric with respect to the origin and is contained in quadrants I and III.
|
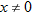 . Therefore, we say the domain is the set of all real numbers excluding zero. The graph of the reciprocal function illustrates that its range is also the set of all real numbers except zero. Note that the reciprocal function is symmetric with respect to the origin and is contained in quadrants I and III.
. Therefore, we say the domain is the set of all real numbers excluding zero. The graph of the reciprocal function illustrates that its range is also the set of all real numbers except zero. Note that the reciprocal function is symmetric with respect to the origin and is contained in quadrants I and III.
|
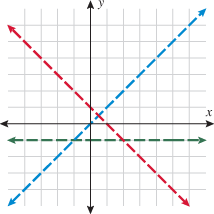
3.2.1.2�Even and Odd Functions
Of the nine functions discussed above, several have similar properties of symmetry. The constant function, square function, and absolute value function are all symmetric with respect to the 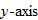 . The identity function, cube function, cube root function, and reciprocal function are all symmetric with respect to the origin. The term even is used to describe functions that are symmetric with respect to the
. The identity function, cube function, cube root function, and reciprocal function are all symmetric with respect to the origin. The term even is used to describe functions that are symmetric with respect to the 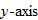 , or vertical axis, and the term odd is used to describe functions that are symmetric with respect to the origin. Recall from Section 2.2 that symmetry can be determined both graphically and algebraically. The box below summarizes the graphic and algebraic characteristics of even and odd functions.
, or vertical axis, and the term odd is used to describe functions that are symmetric with respect to the origin. Recall from Section 2.2 that symmetry can be determined both graphically and algebraically. The box below summarizes the graphic and algebraic characteristics of even and odd functions.
 . The identity function, cube function, cube root function, and reciprocal function are all symmetric with respect to the origin. The term even is used to describe functions that are symmetric with respect to the
. The identity function, cube function, cube root function, and reciprocal function are all symmetric with respect to the origin. The term even is used to describe functions that are symmetric with respect to the 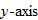 , or vertical axis, and the term odd is used to describe functions that are symmetric with respect to the origin. Recall from Section 2.2 that symmetry can be determined both graphically and algebraically. The box below summarizes the graphic and algebraic characteristics of even and odd functions.
, or vertical axis, and the term odd is used to describe functions that are symmetric with respect to the origin. Recall from Section 2.2 that symmetry can be determined both graphically and algebraically. The box below summarizes the graphic and algebraic characteristics of even and odd functions.
|
The algebraic method for determining symmetry with respect to the  , or vertical axis, is to substitute
, or vertical axis, is to substitute  for
for  . If the result is an equivalent equation, the function is symmetric with respect to the
. If the result is an equivalent equation, the function is symmetric with respect to the 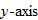 . Some examples of even functions are
. Some examples of even functions are 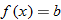 ,
, 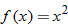 ,
, 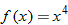 ; and
; and 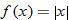 .
.
In any of these equations, if 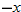 is substituted for
is substituted for  , the result is the same; that is,
, the result is the same; that is, 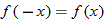 . Also note that, with the exception of the absolute value function, these examples are all even-degree polynomial equations. All constant functions are degree zero and are even functions.
. Also note that, with the exception of the absolute value function, these examples are all even-degree polynomial equations. All constant functions are degree zero and are even functions.
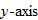 , or vertical axis, is to substitute
, or vertical axis, is to substitute 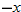 for
for  . If the result is an equivalent equation, the function is symmetric with respect to the
. If the result is an equivalent equation, the function is symmetric with respect to the 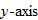 . Some examples of even functions are
. Some examples of even functions are 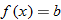 ,
, 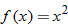 ,
, 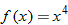 ; and
; and 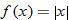 .
.
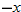 is substituted for
is substituted for  , the result is the same; that is,
, the result is the same; that is, 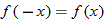 . Also note that, with the exception of the absolute value function, these examples are all even-degree polynomial equations. All constant functions are degree zero and are even functions.
. Also note that, with the exception of the absolute value function, these examples are all even-degree polynomial equations. All constant functions are degree zero and are even functions.The algebraic method for determining symmetry with respect to the origin is to substitute 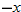 for
for  . If the result is the negative of the original function, that is, if
. If the result is the negative of the original function, that is, if 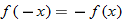 , then the function is symmetric with respect to the origin and, hence, classified as an odd function. Examples of odd functions are
, then the function is symmetric with respect to the origin and, hence, classified as an odd function. Examples of odd functions are 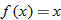 ,
, 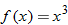 ,
, 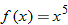 , and
, and 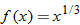 . In any of these functions, if
. In any of these functions, if 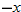 is substituted for
is substituted for  , the result is the negative of the original function. Note that with the exception of the cube root function, these equations are odd-degree polynomials.
, the result is the negative of the original function. Note that with the exception of the cube root function, these equations are odd-degree polynomials.
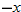 for
for  . If the result is the negative of the original function, that is, if
. If the result is the negative of the original function, that is, if 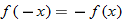 , then the function is symmetric with respect to the origin and, hence, classified as an odd function. Examples of odd functions are
, then the function is symmetric with respect to the origin and, hence, classified as an odd function. Examples of odd functions are 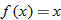 ,
, 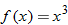 ,
, 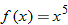 , and
, and 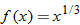 . In any of these functions, if
. In any of these functions, if 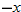 is substituted for
is substituted for  , the result is the negative of the original function. Note that with the exception of the cube root function, these equations are odd-degree polynomials.
, the result is the negative of the original function. Note that with the exception of the cube root function, these equations are odd-degree polynomials.Be careful, though, because functions that are combinations of even- and odd-degree polynomials can turn out to be neither even nor odd, as we will see in Example 1.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Increasing and Decreasing Functions
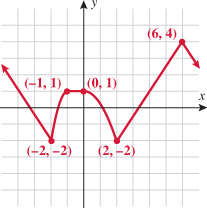
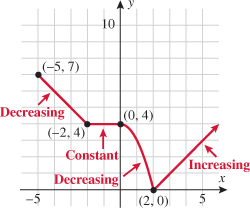
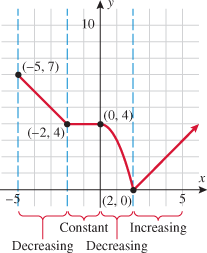
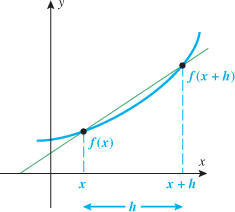
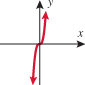
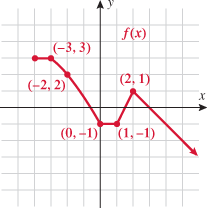
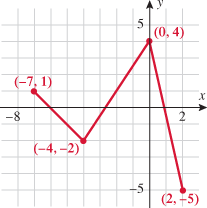
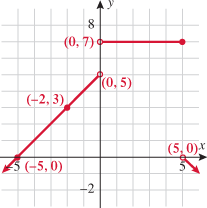
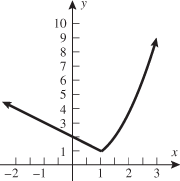
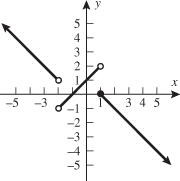
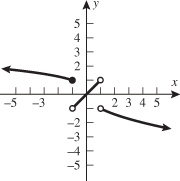
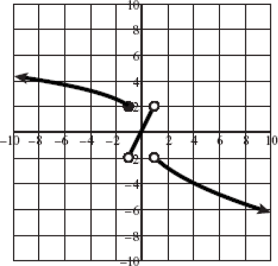
Look at the figure in the margin below. Graphs are read from left to right.
If we start at the left side of the graph and trace the red curve with our pen, we see that the function values (values in the vertical direction) are decreasing until arriving at the point  . Then, the function values increase until arriving at the point
. Then, the function values increase until arriving at the point 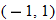 . The values then remain constant
. The values then remain constant  between the points
between the points 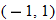 and
and  . Proceeding beyond the point
. Proceeding beyond the point  , the function values decrease again until the point
, the function values decrease again until the point  . Beyond the point
. Beyond the point  , the function values increase again until the point
, the function values increase again until the point  . Finally, the function values decrease and continue to do so.
. Finally, the function values decrease and continue to do so.
 . Then, the function values increase until arriving at the point
. Then, the function values increase until arriving at the point 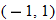 . The values then remain constant
. The values then remain constant  between the points
between the points 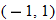 and
and  . Proceeding beyond the point
. Proceeding beyond the point  , the function values decrease again until the point
, the function values decrease again until the point  . Beyond the point
. Beyond the point  , the function values increase again until the point
, the function values increase again until the point  . Finally, the function values decrease and continue to do so.
. Finally, the function values decrease and continue to do so.
|
When specifying a function as increasing, decreasing, or constant, the intervals are classified according to the  .
.
For instance, in this graph, we say the function is increasing when  is between
is between  and
and  and again when
and again when  is between
is between  and
and  . The graph is classified as decreasing when
. The graph is classified as decreasing when  is less than
is less than  and again when
and again when  is between 0 and 2 and again when
is between 0 and 2 and again when  is greater than 6. The graph is classified as constant when
is greater than 6. The graph is classified as constant when  is between
is between  and 0. In interval notation, this is summarized as
and 0. In interval notation, this is summarized as
 .
.
 is between
is between  and
and  and again when
and again when  is between
is between  and
and  . The graph is classified as decreasing when
. The graph is classified as decreasing when  is less than
is less than  and again when
and again when  is between 0 and 2 and again when
is between 0 and 2 and again when  is greater than 6. The graph is classified as constant when
is greater than 6. The graph is classified as constant when  is between
is between  and 0. In interval notation, this is summarized as
and 0. In interval notation, this is summarized as
|
An algebraic test for determining whether a function is increasing, decreasing, or constant is to compare the value  of the function for particular points in the intervals.
of the function for particular points in the intervals.
 of the function for particular points in the intervals.
of the function for particular points in the intervals.
| |||||||||||||||||||
In addition to classifying a function as increasing, decreasing, or constant, we can also determine the domain and range of a function by inspecting its graph from left to right:
|
|||||||||||||||||||||
Average Rate of Change
How do we know how much a function is increasing or decreasing? For example, is the price of a stock slightly increasing or is it doubling every week? One way we determine how much a function is increasing or decreasing is by calculating its average rate of change.
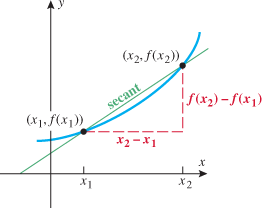
Let  and
and  be two points that lie on the graph of a function
be two points that lie on the graph of a function  . Draw the line that passes through these two points
. Draw the line that passes through these two points  and
and  . This line is called a secant line.
. This line is called a secant line.
 and
and  be two points that lie on the graph of a function
be two points that lie on the graph of a function  . Draw the line that passes through these two points
. Draw the line that passes through these two points  and
and  . This line is called a secant line.
. This line is called a secant line.
|
Note that the slope of the secant line is given by  , and recall that the slope of a line is the rate of change of that line. The slope of the secant line is used to represent the average rate of change of the function.
, and recall that the slope of a line is the rate of change of that line. The slope of the secant line is used to represent the average rate of change of the function.
 , and recall that the slope of a line is the rate of change of that line. The slope of the secant line is used to represent the average rate of change of the function.
, and recall that the slope of a line is the rate of change of that line. The slope of the secant line is used to represent the average rate of change of the function.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The average rate of change can also be written in terms of the difference quotient.
|
When written in this form, the average rate of change is called the difference quotient.
|
|
The difference quotient is more meaningful when  is small. In calculus the difference quotient is used to define a derivative.
is small. In calculus the difference quotient is used to define a derivative.
 is small. In calculus the difference quotient is used to define a derivative.
is small. In calculus the difference quotient is used to define a derivative.
|
Piecewise-Defined Functions
Most of the functions that we have seen in this text are functions defined by polynomials. Sometimes the need arises to define functions in terms of pieces. For example, most plumbers charge a flat fee for a house call and then an additional hourly rate for the job. For instance, if a particular plumber charges  to drive out to your house and work for 1 hour and then an additional
to drive out to your house and work for 1 hour and then an additional  an hour for every additional hour he or she works on your job, we would define this function in pieces. If we let
an hour for every additional hour he or she works on your job, we would define this function in pieces. If we let  be the number of hours worked, then the charge is defined as
be the number of hours worked, then the charge is defined as
 If we were to graph this function, we would see that there is 1 hour that is constant and after that the function continually increases.
If we were to graph this function, we would see that there is 1 hour that is constant and after that the function continually increases.
 to drive out to your house and work for 1 hour and then an additional
to drive out to your house and work for 1 hour and then an additional  an hour for every additional hour he or she works on your job, we would define this function in pieces. If we let
an hour for every additional hour he or she works on your job, we would define this function in pieces. If we let  be the number of hours worked, then the charge is defined as
be the number of hours worked, then the charge is defined as

|
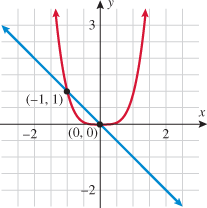
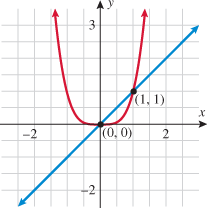
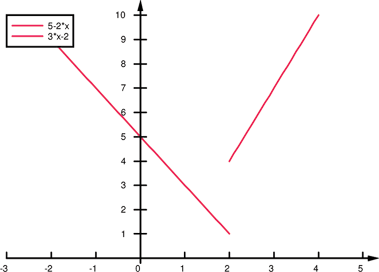
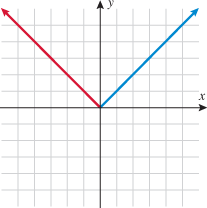
Another piecewise-defined function is the absolute value function. The absolute value function can be thought of as two pieces: the line  (when
(when  is negative) and the line
is negative) and the line  (when
(when  is nonnegative). We start by graphing these two lines on the same graph.
is nonnegative). We start by graphing these two lines on the same graph.
 (when
(when  is negative) and the line
is negative) and the line  (when
(when  is nonnegative). We start by graphing these two lines on the same graph.
is nonnegative). We start by graphing these two lines on the same graph.
|
The absolute value function behaves like the line  when
when  is negative (erase the blue graph in quadrant IV) and like the line
is negative (erase the blue graph in quadrant IV) and like the line  when
when  is positive (erase the red graph in quadrant III).
is positive (erase the red graph in quadrant III).

 when
when  is negative (erase the blue graph in quadrant IV) and like the line
is negative (erase the blue graph in quadrant IV) and like the line  when
when  is positive (erase the red graph in quadrant III).
is positive (erase the red graph in quadrant III).
|

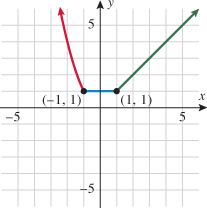
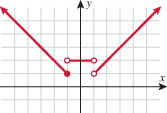
The next example is a piecewise-defined function given in terms of functions in our “library of functions.” Because the function is defined in terms of pieces of other functions, we draw the graph of each individual function, and then for each function, darken the piece corresponding to its part of the domain. This is like the procedure above for the absolute value function.
|
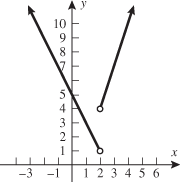
The term continuous implies that there are no holes or jumps and that the graph can be drawn without picking up your pencil. A function that does have holes or jumps and cannot be drawn in one motion without picking up your pencil is classified as discontinuous, and the points where the holes or jumps occur are called points of discontinuity.
The previous example illustrates a continuous piecewise-defined function. At the  junction, the square function and constant function both pass through the point
junction, the square function and constant function both pass through the point 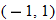 . At the
. At the  junction, the constant function and the identity function both pass through the point
junction, the constant function and the identity function both pass through the point 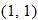 . Since the graph of this piecewise-defined function has no holes or jumps, we classify it as a continuous function.
. Since the graph of this piecewise-defined function has no holes or jumps, we classify it as a continuous function.
 junction, the square function and constant function both pass through the point
junction, the square function and constant function both pass through the point 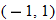 . At the
. At the  junction, the constant function and the identity function both pass through the point
junction, the constant function and the identity function both pass through the point 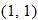 . Since the graph of this piecewise-defined function has no holes or jumps, we classify it as a continuous function.
. Since the graph of this piecewise-defined function has no holes or jumps, we classify it as a continuous function.The next example illustrates a discontinuous piecewise-defined function.
|
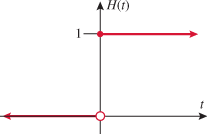
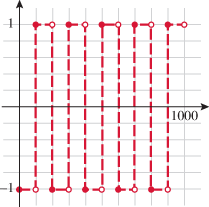
Piecewise-defined functions whose “pieces” are constants are called step functions. The reason for this name is that the graph of a step function looks like steps of a staircase. A common step function used in engineering is the Heaviside step function (also called the unit step function):

This function is used in signal processing to represent a signal that turns on at some time and stays on indefinitely.

|
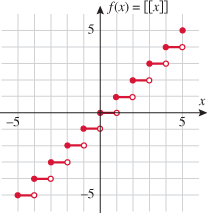
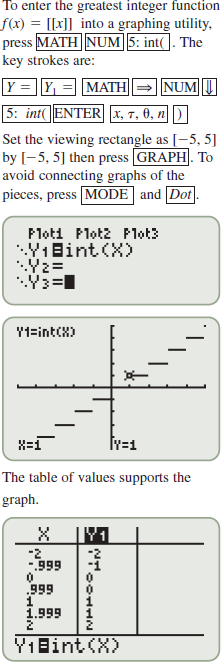
A common step function used in business applications is the greatest integer function.
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
SECTION 3.2 |
EXERCISES |
| SKILLS |
| 1.�� |
 |
| 2.�� |  |
| 3.�� |
 |
| 4.�� |  |
| 5.�� |
 |
| 6.�� |  |
| 7.�� |
 |
| 8.�� |  |
| 9.�� |
 |
| 10.�� |  |
| 11.�� |
 |
| 12.�� |  |
| 13.�� |
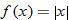 |
| 14.�� |  |
| 15.�� |
 |
| 16.�� |  |
| 17.�� |
 |
| 18.�� |  |
| 19.�� |
 |
| 20.�� |  |
| 21.�� |
 |
| 22.�� |  |
| 23.�� |
|
| 24.�� |
|
| 25.�� |
|
| 26.�� |
|
| 27.�� |
|
| 28.�� |
|
| 29.�� |
|
| 30.�� |
|
| 31.�� |
|
| 32.�� |
|
| 33.�� |
|
| 34.�� |
|
| 35.�� |
|
| 36.�� |
|
| 37.�� |
 |
| 38.�� |  |
| 39.�� |
 |
| 40.�� |  |
| 41.�� |
 |
| 42.�� |  |
| 43.�� |
 |
| 44.�� |  |
| 45.�� |
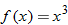 |
| 46.�� |  |
| 47.�� |
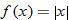 |
| 48.�� |  |
| 49.�� |
 |
| 50.�� |  |
| 51.�� |
 |
| 52.�� |  |
| 53.�� |
 |
| 54.�� |  |
| 55.�� |
 |
| 56.�� |  |
| 57.�� |
 |
| 58.�� |  |
| 59.�� |
 |
| 60.�� |  |
| 61.�� |
 |
| 62.�� |  |
| 63.�� |
 |
| 64.�� |  |
| 65.�� |
 |
| 66.�� |  |
| 67.�� |
 |
| 68.�� |  |
| 69.�� |
 |
| 70.�� |  |
| 71.�� |
 |
| 72.�� |  |
| 73.�� |
 |
| 74.�� |  |
| 75.�� |
 |
| 76.�� |  |
| 77.�� |
 |
| 78.�� |  |
| APPLICATIONS |
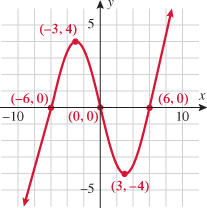
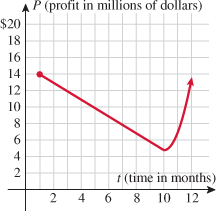
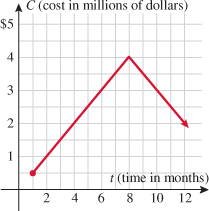
A manufacturer determines that his profit and cost functions over one year are represented by the following graphs.
|
|
| 79.�� |
Business.
Find the intervals on which profit is increasing, decreasing, and constant.
|
| 80.�� |
Business.
Find the intervals on which cost is increasing, decreasing, and constant.
|
| 81.�� |
Budget: Costs.
The Kappa Kappa Gamma sorority decides to order custom-made T-shirts for its Kappa Krush mixer with the Sigma Alpha Epsilon fraternity. If the sorority orders 50 or fewer T-shirts, the cost is
 per shirt. If it orders more than 50 but less than or equal to 100, the cost is per shirt. If it orders more than 50 but less than or equal to 100, the cost is  per shirt. If it orders more than 100, the cost is per shirt. If it orders more than 100, the cost is  per shirt. Find the cost function per shirt. Find the cost function  as a function of the number of T-shirts as a function of the number of T-shirts  ordered. ordered. |
| 82.�� |
Budget: Costs.
The marching band at a university is ordering some additional uniforms to replace existing uniforms that are worn out. If the band orders 50 or fewer, the cost is
 per uniform. If it orders more than 50 but less than or equal to 100, the cost is per uniform. If it orders more than 50 but less than or equal to 100, the cost is  per uniform. Find the cost function per uniform. Find the cost function  as a function of the number of new uniforms as a function of the number of new uniforms  ordered. ordered. |
| 83.�� |
Budget: Costs.
The Richmond rowing club is planning to enter the Head of the Charles race in Boston and is trying to figure out how much money to raise. The entry fee is
 per boat for the first 10 boats and per boat for the first 10 boats and  for each additional boat. Find the cost function for each additional boat. Find the cost function  as a function of the number of boats as a function of the number of boats  the club enters. the club enters. |
| 84.�� |
Phone Cost: Long-Distance Calling.
A phone company charges
 per minute for the first 10 minutes of an international long-distance phone call and per minute for the first 10 minutes of an international long-distance phone call and  per minute every minute after that. Find the cost function per minute every minute after that. Find the cost function  as a function of the length of the phone call as a function of the length of the phone call  in minutes. in minutes. |
| 85.�� |
Event Planning.
A young couple are planning their wedding reception at a yacht club. The yacht club charges a flat rate of
 to reserve the dining room for a private party. The cost of food is to reserve the dining room for a private party. The cost of food is  per person for the first 100 people and per person for the first 100 people and  per person for every additional person beyond the first 100. Write the cost function per person for every additional person beyond the first 100. Write the cost function  as a function of the number of people as a function of the number of people  attending the reception. attending the reception. |
| 86.�� |
Home Improvement.
An irrigation company gives you an estimate for an eight-zone sprinkler system. The parts are
 , and the labor is , and the labor is  per hour. Write a function per hour. Write a function  that determines the cost of a new sprinkler system if you choose this irrigation company. that determines the cost of a new sprinkler system if you choose this irrigation company. |
| 87.�� |
Sales.
A famous author negotiates with her publisher the monies she will receive for her next suspense novel. She will receive
 up front and a up front and a  royalty rate on the first 100,000 books sold, and royalty rate on the first 100,000 books sold, and  on any books sold beyond that. If the book sells for on any books sold beyond that. If the book sells for  and royalties are based on the selling price, write a royalties function and royalties are based on the selling price, write a royalties function  as a function of total number as a function of total number  of books sold. of books sold. |
| 88.�� |
Sales.
Rework Exercise 87 if the author receives
 up front, up front,  for the first 100,000 books sold, and for the first 100,000 books sold, and  on any books sold beyond that. on any books sold beyond that. |
| 89.�� |
Profit.
Some artists are trying to decide whether they will make a profit if they set up a Web-based business to market and sell stained glass that they make. The costs associated with this business are
 per month for the website and per month for the website and  per month for the studio they rent. The materials cost per month for the studio they rent. The materials cost  for each work in stained glass, and the artists charge for each work in stained glass, and the artists charge  for each unit they sell. Write the monthly profit as a function of the number of stained-glass units they sell. for each unit they sell. Write the monthly profit as a function of the number of stained-glass units they sell. |
| 90.�� |
Profit.
Philip decides to host a shrimp boil at his house as a fundraiser for his daughter's AAU basketball team. He orders gulf shrimp to be flown in from New Orleans. The shrimp costs
 per pound. The shipping costs per pound. The shipping costs  . If he charges . If he charges  per person, write a function per person, write a function  that represents either his loss or profit as a function of the number of people that represents either his loss or profit as a function of the number of people  that attend. Assume that each person will eat 1 pound of shrimp. that attend. Assume that each person will eat 1 pound of shrimp. |
| 91.�� |
Postage Rates.
The following table corresponds to first-class postage rates for the U.S. Postal Service. Write a piecewise-defined function in terms of the greatest integer function that models this cost of mailing flat envelopes first class.
|
| 92.�� |
Postage Rates.
The following table corresponds to first-class postage rates for the U.S. Postal Service. Write a piecewise-defined function in terms of the greatest integer function that models this cost of mailing parcels first class.
|
| 93.�� |
Electronics: Signals.
Write a step function  that represents the following square wave. that represents the following square wave.
|
| 94.�� |
Electronics: Signals.
Write a step function  that represents the following square wave, where that represents the following square wave, where  represents frequency in Hz. represents frequency in Hz.
|
| 95.�� |
Climate Change: Global Warming.
What is the average rate of change in global carbon emissions from fossil fuel burning from
|
| 96.�� |
Climate Change: Global Warming.
What is the average rate of change in global carbon emissions from fossil fuel burning from
|
The height (in feet) of a falling object with an initial velocity of  per second launched straight upward from the ground is given by
per second launched straight upward from the ground is given by  , where
, where  is time (in seconds).
is time (in seconds).
 per second launched straight upward from the ground is given by
per second launched straight upward from the ground is given by  , where
, where  is time (in seconds).
is time (in seconds).| 97.�� |
Falling Objects.
What is the average rate of change of the height as a function of time from
 to to  ? ? |
| 98.�� |
Falling Objects.
What is the average rate of change of the height as a function of time from
 to to  ? ? |
An analysis of sales indicates that demand for a product during a calendar year (no leap year) is modeled by
 where
where  is demand in thousands of units and
is demand in thousands of units and  is the day of the year and
is the day of the year and  represents January 1.
represents January 1.

 is demand in thousands of units and
is demand in thousands of units and  is the day of the year and
is the day of the year and  represents January 1.
represents January 1.| 99.�� |
Economics.
Find the average rate of change of the demand of the product over the first quarter.
|
| 100.�� |
Economics.
Find the average rate of change of the demand of the product over the fourth quarter.
|
| CATCH THE MISTAKE |
| 101.�� |
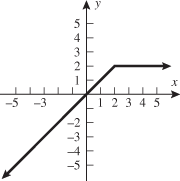
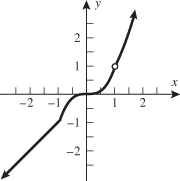
Graph the piecewise-defined function. State the domain and range.

Solution:
Draw the graphs of
 and and  . .
 when when  and the function and the function  when when  . This gives us the familiar absolute value graph. . This gives us the familiar absolute value graph.
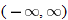 or or 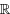 Range: Range: 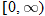
This is incorrect. What mistake was made?
|
| 102.�� |
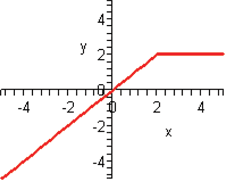
Graph the piecewise-defined function. State the domain and range.

Solution:
Draw the graphs of
 and and  . .
 when when  and the function and the function  when when  . .
Domain:
 or or 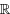 Range: Range: 
This is incorrect. What mistake was made?
|
| 103.�� |
The cost of airport Internet access is
 for the first 30 minutes and for the first 30 minutes and  per minute for each additional minute. Write a function describing the cost of the service as a function of minutes used online. per minute for each additional minute. Write a function describing the cost of the service as a function of minutes used online.Solution:

|
| 104.�� |
Most money market accounts pay a higher interest with a higher principal. If the credit union is offering
 on accounts with less than or equal to on accounts with less than or equal to  and and  on the additional money over on the additional money over  , write the interest function , write the interest function  that represents the interest earned on an account as a function of dollars in the account. that represents the interest earned on an account as a function of dollars in the account.Solution:

|
| CONCEPTUAL |
| 105.�� |
The identity function is a special case of the linear function. |
| 106.�� | The constant function is a special case of the linear function. |
| 107.�� |
If an odd function has an interval where the function is increasing, then it also has to have an interval where the function is decreasing. |
| 108.�� | If an even function has an interval where the function is increasing, then it also has to have an interval where the function is decreasing. |
| CHALLENGE |
| 109.�� |
 |
| 110.�� |  |
| TECHNOLOGY |
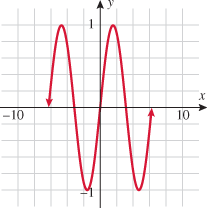
| 111.�� |
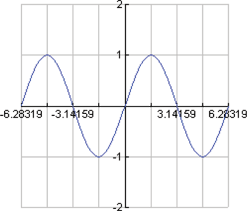
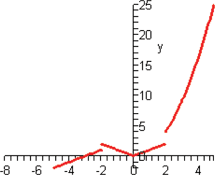
In trigonometry you will learn about the sine function,  . Plot the function . Plot the function  , using a graphing utility. It should look like the graph on the right. Is the sine function even, odd, or neither? , using a graphing utility. It should look like the graph on the right. Is the sine function even, odd, or neither?
|
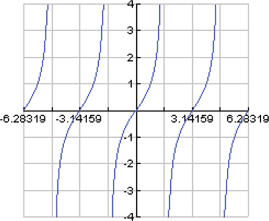
| 112.�� | In trigonometry you will learn about the cosine function,  . Plot the function . Plot the function  , using a graphing utility. It should look like the graph on the right. Is the cosine function even, odd, or neither? , using a graphing utility. It should look like the graph on the right. Is the cosine function even, odd, or neither?
|
| 113.�� |
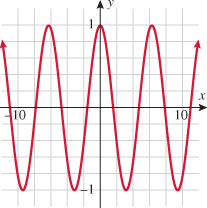
In trigonometry you will learn about the tangent function,  . Plot the function . Plot the function  , using a graphing utility. If you restrict the values of , using a graphing utility. If you restrict the values of  so that so that  , the graph should resemble the graph below. Is the tangent function even, odd, or neither? , the graph should resemble the graph below. Is the tangent function even, odd, or neither?
|
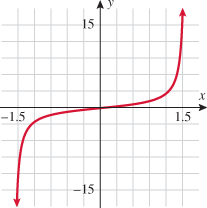
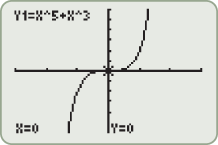
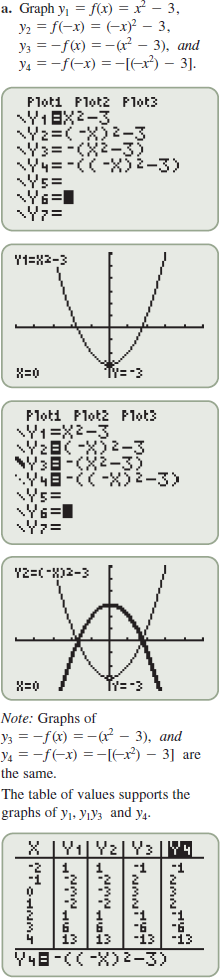
| 114.�� | Plot the function
 . What function is this? . What function is this? |
| 115.�� |
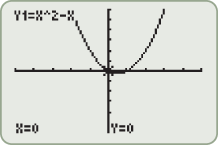
Graph the function
 using a graphing utility. State the domain and range. using a graphing utility. State the domain and range. |
| 116.�� | Graph the function
 using a graphing utility. State the domain and range. using a graphing utility. State the domain and range. |












 or
or 






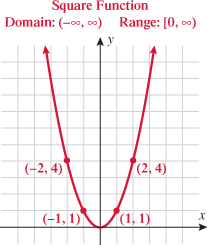




 �Technology Tip
�Technology Tip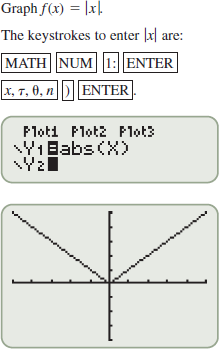
 .
.
 .
.
 .
.




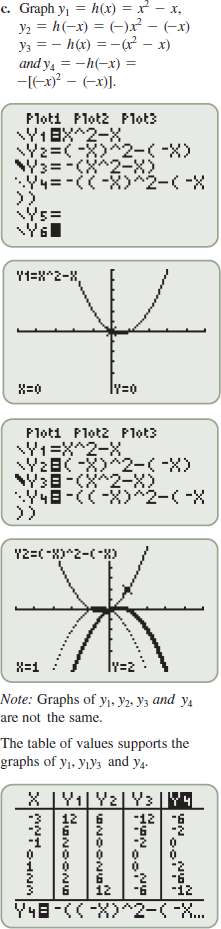



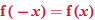 , we say that
, we say that 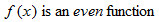 .
.


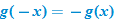 , we say that
, we say that 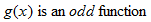 .
.


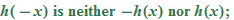 therefore the function
therefore the function  is
is  .
.



 .
.


 is
is  if for any
if for any  and
and  in
in  , then
, then  .
. .
. .
. (from bottom to top) that the graph of the function corresponds to.
(from bottom to top) that the graph of the function corresponds to.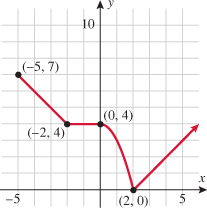

 to the point
to the point  .
. .
. .
. .
.

 is included in the domain of the function but not in the interval where the function is classified as decreasing.
is included in the domain of the function but not in the interval where the function is classified as decreasing.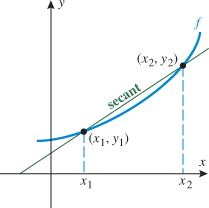
 and
and  be two distinct points,
be two distinct points,  , on the graph of the function
, on the graph of the function 


 and
and  .
.
 and
and  .
.


 and
and  .
.
 .
.

 and
and  .
.
 and
and  .
.


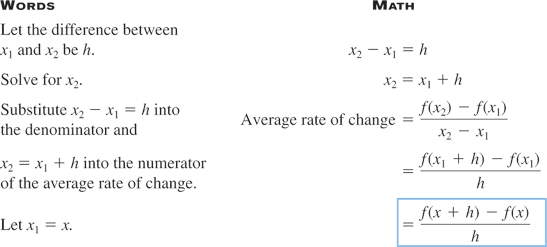
 , where
, where  , is called the
, is called the  .
.

 .
.
 menu operations to define the inequalities in the function. Press:
menu operations to define the inequalities in the function. Press:

 by
by  ; then press
; then press  .
.




 , this function is defined by the square function,
, this function is defined by the square function,  , the function is defined by the constant function,
, the function is defined by the constant function,  . The intervals of increasing, decreasing, and constant are as follows:
. The intervals of increasing, decreasing, and constant are as follows:


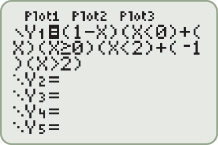
 and
and  . Set the viewing rectangle as
. Set the viewing rectangle as  and
and 



 the function is defined by the
the function is defined by the  , the function is defined by the
, the function is defined by the  , the function is defined by the
, the function is defined by the 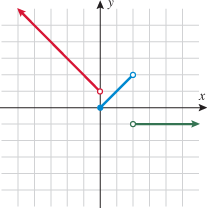
 .
.




 and the additional single value
and the additional single value  .
.

 at
at 



 .
.


 or
or 










 So, not even.
So, not even.  So, not odd. Thus,
So, not odd. Thus,  .
. So,
So,  . Thus,
. Thus, 

 .
.




 So,
So, 







 .
. .
. .
.
 , (e)
, (e)  , and (f)
, and (f)  .
.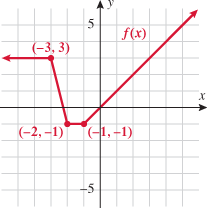

 ,
constant:
,
constant: 







 , decreasing:
, decreasing:  , constant: nowhere
, constant: nowhere





 , decreasing: nowhere,
constant:
, decreasing: nowhere,
constant: 


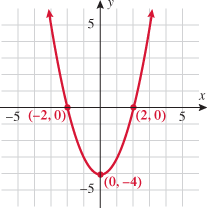

 , decreasing:
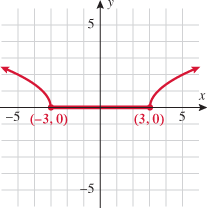
, decreasing:  , constant: nowhere
, constant: nowhere



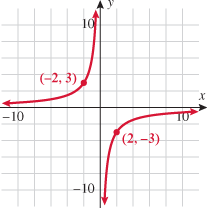



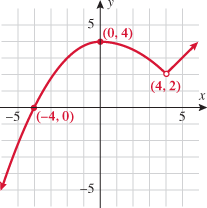
 or
or 
 , constant
, constant 











 .
.







































 , and
, and  , and a closed hole at
, and a closed hole at 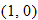 .
.
 .
.













 and closed holes at
and closed holes at  .
.
 .
.
 to
to  , which corresponds to Oct. to Dec.
, which corresponds to Oct. to Dec. to
to 
 . The cost function is given by
. The cost function is given by


 . The cost function is given by
. The cost function is given by


 . The cost function is given by
. The cost function is given by



 .
. , the amount of money earned for
, the amount of money earned for  .
.


 .
. .
.

 where
where 
 .
.






 . So, the average rate of change in
. So, the average rate of change in  during the first quarter is
during the first quarter is


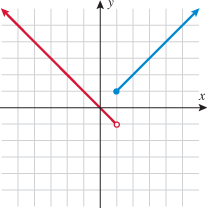
 is not in the domain. The range should be
is not in the domain. The range should be  .
.

 for
for  should be:
should be: 
 with
with  .
. is always increasing.
is always increasing. and
and 
 , are continuous on
, are continuous on  with which we need to be concerned regarding the continuity of
with which we need to be concerned regarding the continuity of  . For
. For  , which is the same as
, which is the same as  .
.
 .
.