|
SECTION 3.1 |
Functions |
| ||||||||||||||||||||||||||||||||||||
 �
�Relations and Functions
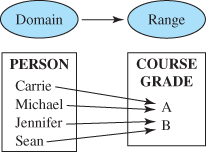
What do the following pairs have in common?
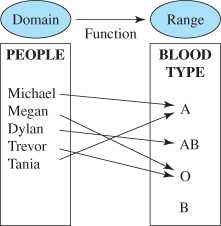
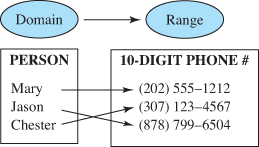
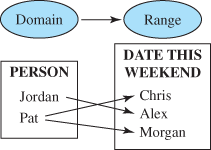
They all describe a particular correspondence between two groups. A relation is a correspondence between two sets. The first set is called the domain, and the corresponding second set is called the range. Members of these sets are called elements.
|
|||||||||||||||||||||
|
A relation is a set of ordered pairs. The domain is the set of all the first components of the ordered pairs, and the range is the set of all the second components of the ordered pairs.
A relation in which each element in the domain corresponds to exactly one element in the range is a function.
|
|
|
Note that the definition of a function is more restrictive than the definition of a relation. For a relation, each input corresponds to at least one output, whereas, for a function, each input corresponds to exactly one output. The blood-type example given is both a relation and a function.
|
Also note that the range (set of values to which the elements of the domain correspond) is a subset of the set of all blood types. However, although all functions are relations, not all relations are functions.
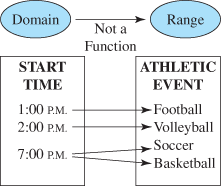
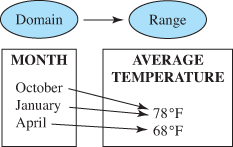
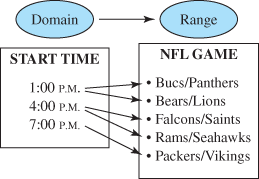
For example, at a university, four primary sports typically overlap in the late fall: football, volleyball, soccer, and basketball. On a given Saturday, the following table indicates the start times for the competitions.
Because an element in the domain, 7:00 p.m., corresponds to more than one element in the range, Soccer and Basketball, this is not a function. It is, however, a relation.
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||
All of the examples we have discussed thus far are discrete sets in that they represent a countable set of distinct pairs of 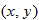 . A function can also be defined algebraically by an equation.
. A function can also be defined algebraically by an equation.
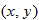 . A function can also be defined algebraically by an equation.
. A function can also be defined algebraically by an equation.Functions Defined by Equations
Let's start with the equation 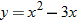 , where
, where  can be any real number. This equation assigns to each
can be any real number. This equation assigns to each 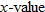 exactly one corresponding
exactly one corresponding  .
.
Since the variable  depends on what value of
depends on what value of  is selected, we denote
is selected, we denote  as the dependent variable. The variable
as the dependent variable. The variable  can be any number in the domain; therefore, we denote
can be any number in the domain; therefore, we denote  as the independent variable.
as the independent variable.
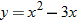 , where
, where  can be any real number. This equation assigns to each
can be any real number. This equation assigns to each 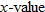 exactly one corresponding
exactly one corresponding  .
.
|
 depends on what value of
depends on what value of  is selected, we denote
is selected, we denote  as the dependent variable. The variable
as the dependent variable. The variable  can be any number in the domain; therefore, we denote
can be any number in the domain; therefore, we denote  as the independent variable.
as the independent variable.Although functions are defined by equations, it is important to recognize that not all equations are functions.
The requirement for an equation to define a function is that each element in the domain corresponds to exactly one element in the range. Throughout the ensuing discussion, we assume 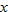 to be the independent variable and
to be the independent variable and 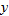 to be the dependent variable.
to be the dependent variable.
In the “equations that represent functions of  ,” every
,” every 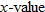 corresponds to exactly one
corresponds to exactly one  . Some ordered pairs that correspond to these functions are
. Some ordered pairs that correspond to these functions are
The fact that  and
and  both correspond to
both correspond to 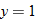 in the first two examples does not violate the definition of a function.
in the first two examples does not violate the definition of a function.
|
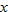 to be the independent variable and
to be the independent variable and 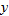 to be the dependent variable.
to be the dependent variable.
|
 ,” every
,” every 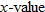 corresponds to exactly one
corresponds to exactly one  . Some ordered pairs that correspond to these functions are
. Some ordered pairs that correspond to these functions are
|
 and
and  both correspond to
both correspond to 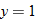 in the first two examples does not violate the definition of a function.
in the first two examples does not violate the definition of a function.In the “equations that do not represent functions of  ,” some
,” some 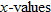 correspond to more than one
correspond to more than one  .
.
Some ordered pairs that correspond to these equations are
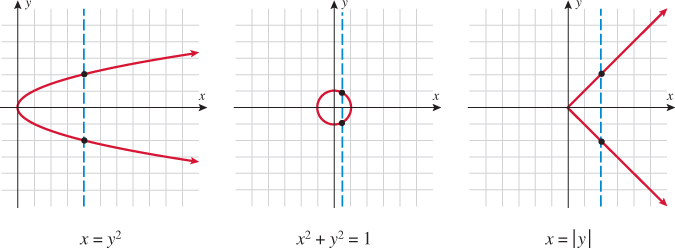
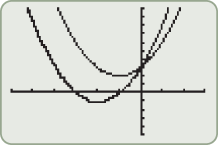
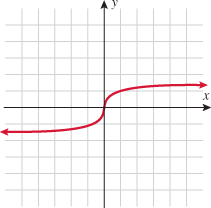
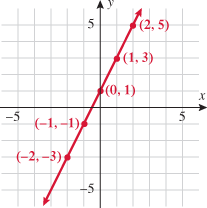
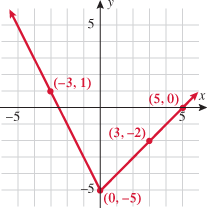
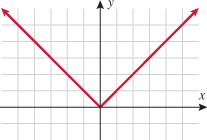
Let's look at the graphs of the three functions of  :
:
Let's take any value for  , say
, say 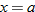 . The graph of
. The graph of 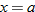 corresponds to a vertical line. A function of
corresponds to a vertical line. A function of  maps each
maps each 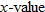 to exactly one
to exactly one  ; therefore, there should be at most one point of intersection with any vertical line. We see in the three graphs of the functions above that if a vertical line is drawn at any value of
; therefore, there should be at most one point of intersection with any vertical line. We see in the three graphs of the functions above that if a vertical line is drawn at any value of 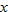 on any of the three graphs, the vertical line only intersects the graph in one place. Look at the graphs of the three equations that do not represent functions of
on any of the three graphs, the vertical line only intersects the graph in one place. Look at the graphs of the three equations that do not represent functions of  .
.
A vertical line can be drawn on any of the three graphs such that the vertical line will intersect each of these graphs at two points. Thus, there are two 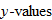 that correspond to some
that correspond to some 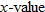 in the domain, which is why these equations do not define
in the domain, which is why these equations do not define 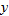 as a function of
as a function of  .
.
 ,” some
,” some 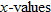 correspond to more than one
correspond to more than one  .
.
|
 :
:
|
 , say
, say 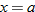 . The graph of
. The graph of 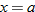 corresponds to a vertical line. A function of
corresponds to a vertical line. A function of  maps each
maps each 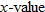 to exactly one
to exactly one  ; therefore, there should be at most one point of intersection with any vertical line. We see in the three graphs of the functions above that if a vertical line is drawn at any value of
; therefore, there should be at most one point of intersection with any vertical line. We see in the three graphs of the functions above that if a vertical line is drawn at any value of 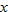 on any of the three graphs, the vertical line only intersects the graph in one place. Look at the graphs of the three equations that do not represent functions of
on any of the three graphs, the vertical line only intersects the graph in one place. Look at the graphs of the three equations that do not represent functions of  .
.
|
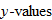 that correspond to some
that correspond to some 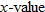 in the domain, which is why these equations do not define
in the domain, which is why these equations do not define 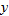 as a function of
as a function of  .
.
|
To recap, a function can be expressed one of four ways: verbally, numerically, algebraically, and graphically. This is sometimes called the Rule of 4.
Expressing a Function | |||||||||
|
Function Notation
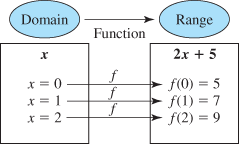
We know that the equation 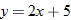 defines
defines  as a function of
as a function of  because its graph is a nonvertical line and thus passes the vertical line test. We can select
because its graph is a nonvertical line and thus passes the vertical line test. We can select  (input) and determine unique corresponding
(input) and determine unique corresponding  (output). The output is found by taking 2 times the input and then adding 5. If we give the function a name, say, “
(output). The output is found by taking 2 times the input and then adding 5. If we give the function a name, say, “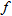 ”, then we can use function notation:
”, then we can use function notation:
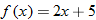 The symbol
The symbol  is read “
is read “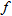 evaluated at
evaluated at  ” or “
” or “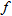 of
of  ” and represents the
” and represents the  that corresponds to a particular
that corresponds to a particular 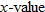 . In other words,
. In other words, 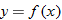 .
.
It is important to note that 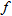 is the function name, whereas
is the function name, whereas  is the value of the function. In other words, the function
is the value of the function. In other words, the function 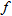 maps some value
maps some value  in the domain to some value
in the domain to some value  in the range.
in the range.
The independent variable is also referred to as the argument of a function. To evaluate functions, it is often useful to think of the independent variable or argument as a placeholder. For example, 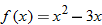 can be thought of as
can be thought of as
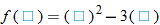 In other words, “
In other words, “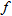 of the argument is equal to the argument squared minus 3 times the argument.” Any expression can be substituted for the argument:
of the argument is equal to the argument squared minus 3 times the argument.” Any expression can be substituted for the argument:
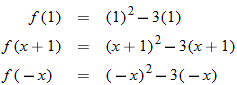 It is important to note:
It is important to note:
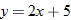 defines
defines  as a function of
as a function of  because its graph is a nonvertical line and thus passes the vertical line test. We can select
because its graph is a nonvertical line and thus passes the vertical line test. We can select 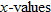 (input) and determine unique corresponding
(input) and determine unique corresponding  (output). The output is found by taking 2 times the input and then adding 5. If we give the function a name, say, “
(output). The output is found by taking 2 times the input and then adding 5. If we give the function a name, say, “ ”, then we can use function notation:
”, then we can use function notation:
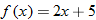
 is read “
is read “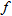 evaluated at
evaluated at  ” or “
” or “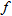 of
of  ” and represents the
” and represents the  that corresponds to a particular
that corresponds to a particular 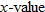 . In other words,
. In other words, 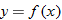 .
.
|
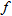 is the function name, whereas
is the function name, whereas  is the value of the function. In other words, the function
is the value of the function. In other words, the function 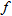 maps some value
maps some value  in the domain to some value
in the domain to some value  in the range.
in the range.
|
|
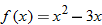 can be thought of as
can be thought of as
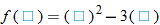
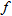 of the argument is equal to the argument squared minus 3 times the argument.” Any expression can be substituted for the argument:
of the argument is equal to the argument squared minus 3 times the argument.” Any expression can be substituted for the argument:
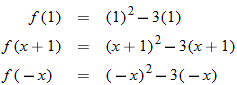
|
||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Now that we have shown that 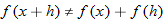 , we turn our attention to one of the fundamental expressions in calculus: the difference quotient.
, we turn our attention to one of the fundamental expressions in calculus: the difference quotient.
 Example 9 illustrates the difference quotient, which will be discussed in detail in Section 3.2. For now, we will concentrate on the algebra involved when finding the difference quotient. In Section 3.2, the application of the difference quotient will be the emphasis.
Example 9 illustrates the difference quotient, which will be discussed in detail in Section 3.2. For now, we will concentrate on the algebra involved when finding the difference quotient. In Section 3.2, the application of the difference quotient will be the emphasis.
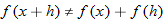 , we turn our attention to one of the fundamental expressions in calculus: the difference quotient.
, we turn our attention to one of the fundamental expressions in calculus: the difference quotient.

|
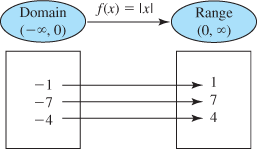
Domain of a Function
Sometimes the domain of a function is stated explicitly. For example,
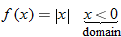 Here, the explicit domain is the set of all negative real numbers,
Here, the explicit domain is the set of all negative real numbers,  . Every negative real number in the domain is mapped to a positive real number in the range through the absolute value function.
. Every negative real number in the domain is mapped to a positive real number in the range through the absolute value function.
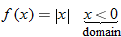
 . Every negative real number in the domain is mapped to a positive real number in the range through the absolute value function.
. Every negative real number in the domain is mapped to a positive real number in the range through the absolute value function.
|
If the expression that defines the function is given but the domain is not stated explicitly, then the domain is implied. The implicit domain is the largest set of real numbers for which the function is defined and the output value  is a real number. For example,
is a real number. For example,
 does not have the domain explicitly stated. There is, however, an implicit domain. Note that if the argument is negative, that is, if
does not have the domain explicitly stated. There is, however, an implicit domain. Note that if the argument is negative, that is, if  , then the result is an imaginary number. In order for the output of the function,
, then the result is an imaginary number. In order for the output of the function,  , to be a real number, we must restrict the domain to nonnegative numbers, that is, if
, to be a real number, we must restrict the domain to nonnegative numbers, that is, if 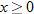 .
.
In general, we ask the question, “what can  be?” The implicit domain of a function excludes values that cause a function to be undefined or have outputs that are not real numbers.
be?” The implicit domain of a function excludes values that cause a function to be undefined or have outputs that are not real numbers.
 is a real number. For example,
is a real number. For example,

 , then the result is an imaginary number. In order for the output of the function,
, then the result is an imaginary number. In order for the output of the function,  , to be a real number, we must restrict the domain to nonnegative numbers, that is, if
, to be a real number, we must restrict the domain to nonnegative numbers, that is, if 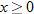 .
.
|
 be?” The implicit domain of a function excludes values that cause a function to be undefined or have outputs that are not real numbers.
be?” The implicit domain of a function excludes values that cause a function to be undefined or have outputs that are not real numbers.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.1.4.1�Applications
Functions that are used in applications often have restrictions on the domains due to physical constraints. For example, the volume of a cube is given by the function 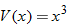 , where
, where 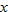 is the length of a side. The function
is the length of a side. The function 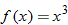 has no restrictions on
has no restrictions on 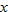 , and therefore the domain is the set of all real numbers. However, the volume of any cube has the restriction that the length of a side can never be negative or zero.
, and therefore the domain is the set of all real numbers. However, the volume of any cube has the restriction that the length of a side can never be negative or zero.
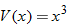 , where
, where 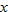 is the length of a side. The function
is the length of a side. The function 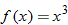 has no restrictions on
has no restrictions on 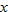 , and therefore the domain is the set of all real numbers. However, the volume of any cube has the restriction that the length of a side can never be negative or zero.
, and therefore the domain is the set of all real numbers. However, the volume of any cube has the restriction that the length of a side can never be negative or zero.
| ||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||
|
SECTION 3.1 |
EXERCISES |
| SKILLS |
| 1.�� |
|
| 2.�� |
|
| 3.�� |
|
| 4.�� |
|
| 5.�� |
|
| 6.�� |
|
| 7.�� |
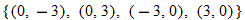 |
| 8.�� | 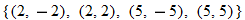 |
| 9.�� |
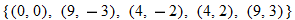 |
| 10.�� | 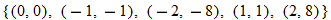 |
| 11.�� |
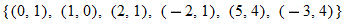 |
| 12.�� | 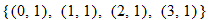 |
| 13.�� |
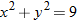 |
| 14.�� | 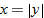 |
| 15.�� |
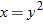 |
| 16.�� | 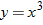 |
| 17.�� |
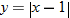 |
| 18.�� | 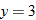 |
| 19.�� |
|
| 20.�� |
|
| 21.�� |
|
| 22.�� |
|
| 23.�� |
|
| 24.�� |
|
| 25.�� | 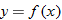
|
| 26.�� | 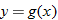
|
| 27.�� | 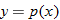
|
| 28.�� | 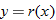
|
| 29.�� | 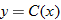
|
| 30.�� | 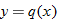
|
| 31.�� | 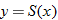
|
| 32.�� | 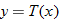
|
| 33.�� |
|
| 34.�� |
| 35.�� |
|
| 36.�� |
| 37.�� |
|
| 38.�� |
| 39.�� |
|
| 40.�� |
| 41.�� |
 |
| 42.�� | 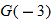 |
| 43.�� |
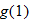 |
| 44.�� | 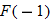 |
| 45.�� |
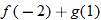 |
| 46.�� | 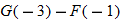 |
| 47.�� |
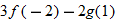 |
| 48.�� | 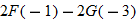 |
| 49.�� |
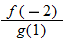 |
| 50.�� | 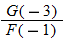 |
| 51.�� |
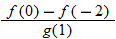 |
| 52.�� | 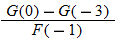 |
| 53.�� |
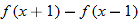 |
| 54.�� | 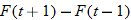 |
| 55.�� |
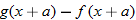 |
| 56.�� | 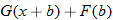 |
| 57.�� |
 |
| 58.�� | 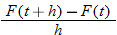 |
| 59.�� |
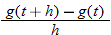 |
| 60.�� | 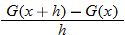 |
| 61.�� |
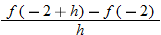 |
| 62.�� | 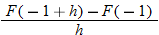 |
| 63.�� |
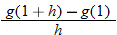 |
| 64.�� | 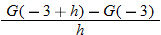 |
| 65.�� |
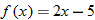 |
| 66.�� | 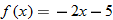 |
| 67.�� |
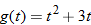 |
| 68.�� | 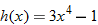 |
| 69.�� |
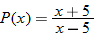 |
| 70.�� | 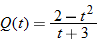 |
| 71.�� |
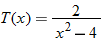 |
| 72.�� | 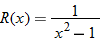 |
| 73.�� |
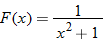 |
| 74.�� | 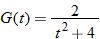 |
| 75.�� |
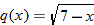 |
| 76.�� | 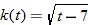 |
| 77.�� |
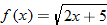 |
| 78.�� | 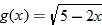 |
| 79.�� |
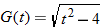 |
| 80.�� | 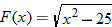 |
| 81.�� |
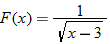 |
| 82.�� | 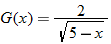 |
| 83.�� |
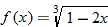 |
| 84.�� | 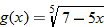 |
| 85.�� |
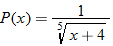 |
| 86.�� | 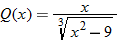 |
| 87.�� |
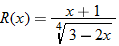 |
| 88.�� | 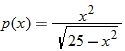 |
| 89.�� |
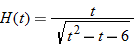 |
| 90.�� | 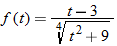 |
| 91.�� |
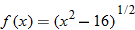 |
| 92.�� | 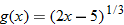 |
| 93.�� |
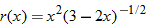 |
| 94.�� | 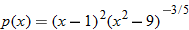 |
| 95.�� |
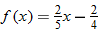 |
| 96.�� | 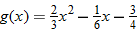 |
| 97.�� |
Let
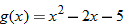 and find the values of and find the values of  that correspond to that correspond to 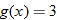 . . |
| 98.�� | Let
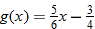 and find the value of and find the value of 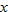 that corresponds to that corresponds to 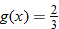 . . |
| 99.�� |
Let
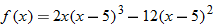 and find the values of and find the values of 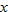 that correspond to that correspond to 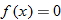 . . |
| 100.�� | Let
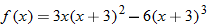 and find the values of and find the values of 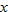 that correspond to that correspond to 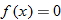 . . |
| APPLICATIONS |
| 101.�� |
Budget: Event Planning.
The cost associated with a catered wedding reception is
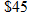 per person for a reception for more than 75 people. Write the cost of the reception in terms of the number of guests and state any domain restrictions. per person for a reception for more than 75 people. Write the cost of the reception in terms of the number of guests and state any domain restrictions. |
| 102.�� |
Budget: Long-Distance Calling.
The cost of a local home phone plan is
 for basic service and for basic service and 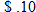 per minute for any domestic long-distance calls. Write the cost of monthly phone service in terms of the number of monthly long-distance minutes and state any domain restrictions. per minute for any domestic long-distance calls. Write the cost of monthly phone service in terms of the number of monthly long-distance minutes and state any domain restrictions. |
| 103.�� |
Temperature.
The average temperature in Tampa, Florida, in the springtime is given by the function
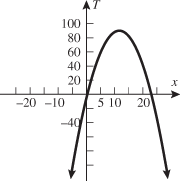
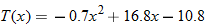 , where , where  is the temperature in degrees Fahrenheit and is the temperature in degrees Fahrenheit and  is the time of day in military time and is restricted to is the time of day in military time and is restricted to 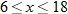 (sunrise to sunset). What is the temperature at 6 a.m.? What is the temperature at noon? (sunrise to sunset). What is the temperature at 6 a.m.? What is the temperature at noon? |
| 104.�� |
Falling Objects: Firecrackers.
A firecracker is launched straight up, and its height is a function of time,
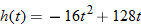 , where , where  is the height in feet and is the height in feet and  is the time in seconds with is the time in seconds with 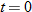 corresponding to the instant it launches. What is the height 4 seconds after launch? What is the domain of this function? corresponding to the instant it launches. What is the height 4 seconds after launch? What is the domain of this function? |
| 105.�� |
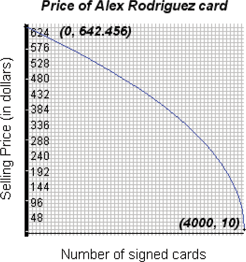
Collectibles.
The price of a signed Alex Rodriguez baseball card is a function of how many are for sale. When Rodriguez was traded from the Texas Rangers to the New York Yankees in 2004, the going rate for a signed baseball card on eBay was
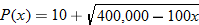 , where , where 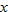 represents the number of signed cards for sale. What was the value of the card when there were 10 signed cards for sale? What was the value of the card when there were 100 signed cards for sale? represents the number of signed cards for sale. What was the value of the card when there were 10 signed cards for sale? What was the value of the card when there were 100 signed cards for sale? |
| 106.�� |
Collectibles.
In Exercise 105, what was the lowest price on eBay, and how many cards were available then? What was the highest price on eBay, and how many cards were available then?
|
| 107.�� |
Volume.
An open box is constructed from a square 10-inch piece of cardboard by cutting squares of length
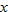 inches out of each corner and folding the sides up. Express the volume of the box as a function of inches out of each corner and folding the sides up. Express the volume of the box as a function of 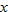 , and state the domain. , and state the domain. |
| 108.�� |
Volume.
A cylindrical water basin will be built to harvest rainwater. The basin is limited in that the largest radius it can have is
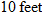 . Write a function representing the volume of water . Write a function representing the volume of water  as a function of height as a function of height  . How many additional gallons of water will be collected if you increase the height by . How many additional gallons of water will be collected if you increase the height by 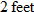 ? ?
Hint:
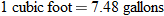 . . |
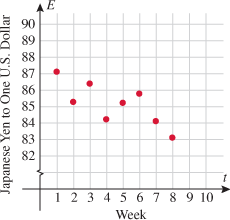
The weekly exchange rate of the U.S. dollar to the Japanese yen is shown in the graph as varying over an 8-week period. Assume the exchange rate 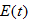 is a function of time (week); let
is a function of time (week); let 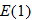 be the exchange rate during Week 1.
be the exchange rate during Week 1.
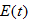 is a function of time (week); let
is a function of time (week); let 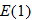 be the exchange rate during Week 1.
be the exchange rate during Week 1.
|
| 109.�� |
Economics.
Approximate the exchange rates of the U.S. dollar to the nearest yen during Weeks 4, 7, and 8.
|
| 110.�� |
Economics.
Find the increase or decrease in the number of Japanese yen to the U.S. dollar exchange rate, to the nearest yen, from (a) Week 2 to Week 3 and (b) Week 6 to Week 7.
|
An epidemiological study of the spread of malaria in a rural area finds that the total number 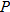 of people who contracted malaria
of people who contracted malaria  days into an outbreak is modeled by the function
days into an outbreak is modeled by the function
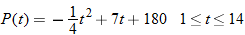
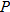 of people who contracted malaria
of people who contracted malaria  days into an outbreak is modeled by the function
days into an outbreak is modeled by the function
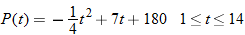
| 111.�� |
Medicine/Health.
How many people have contracted malaria 14 days into the outbreak?
|
| 112.�� |
Medicine/Health.
How many people have contracted malaria 6 days into the outbreak?
|
| 113.�� |
Environment: Tossing the Envelopes.
The average American adult receives 24 pieces of mail per week, usually of some combination of ads and envelopes with windows. Suppose each of these adults throws away a dozen envelopes per week.
|
| 114.�� |
Environment: Tossing the Envelopes.
Each month, Jack receives his bank statement in a 9.5 inch by 6 inch envelope. Each month, he throws away the envelope after removing the statement.
|
| 115.�� |
Finance.
Is the relation whose domain is the year and whose range is the average federal funds rate for the month of January a function? Explain.
|
| 116.�� |
Finance.
Write five ordered pairs whose domain is the set of even years from 2000 to 2008 and whose range is the set of corresponding average federal funds rate for the month of January.
|
| 117.�� |
Health Care Costs.
Fill in the following table. Round dollars to the nearest
 . .
|
| 118.�� |
Health Care Costs.
Using the table found in Exercise 117, let the years correspond to the domain and the total costs correspond to the range. Is this relation a function? Explain.
|
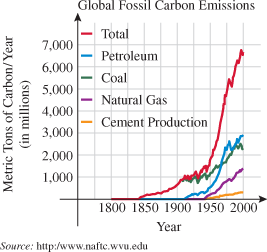
For Exercises 119 and 120, use the following information:
Let the functions 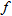 ,
, 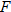 ,
, 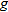 ,
, 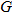 , and
, and 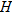 represent the number of tons of carbon emitted per year as a function of year corresponding to cement production, natural gas, coal, petroleum, and the total amount, respectively. Let
represent the number of tons of carbon emitted per year as a function of year corresponding to cement production, natural gas, coal, petroleum, and the total amount, respectively. Let  represent the year, with
represent the year, with 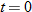 corresponding to 1900.
corresponding to 1900.
|
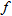 ,
, 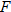 ,
, 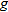 ,
, 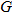 , and
, and 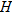 represent the number of tons of carbon emitted per year as a function of year corresponding to cement production, natural gas, coal, petroleum, and the total amount, respectively. Let
represent the number of tons of carbon emitted per year as a function of year corresponding to cement production, natural gas, coal, petroleum, and the total amount, respectively. Let  represent the year, with
represent the year, with 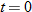 corresponding to 1900.
corresponding to 1900.| 119.�� |
Environment: Global Climate Change.
Estimate (to the nearest thousand) the value of
|
| 120.�� |
Environment: Global Climate Change.
Explain what the sum
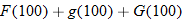 represents. represents. |
| CATCH THE MISTAKE |
| 121.�� |
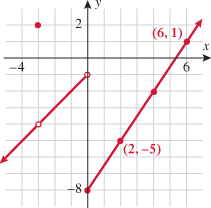
Determine whether the relationship is a function.
Solution:
Apply the horizontal line test.
Because the horizontal line intersects the graph in two places, this is not a function.
|
| 122.�� |
Given the function
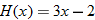 , evaluate the quantity , evaluate the quantity 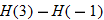 . .Solution:
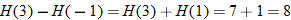 This is incorrect. What mistake was made?
|
| 123.�� |
Given the function
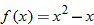 , evaluate the quantity , evaluate the quantity 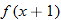 . .Solution:
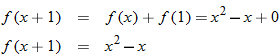 This is incorrect. What mistake was made?
|
| 124.�� |
Determine the domain of the function
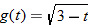 and express it in interval notation. and express it in interval notation.Solution:
What can
 be? Any nonnegative real number. be? Any nonnegative real number.
|
||||||||||||||
| 125.�� |
Given the function
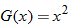 , evaluate , evaluate 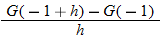 . .Solution:
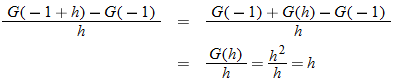
|
| 126.�� |
Given the functions
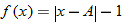 and and 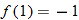 , find , find  . .Solution:
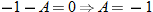 . .This is incorrect. What mistake was made?
|
| CONCEPTUAL |
| 127.�� |
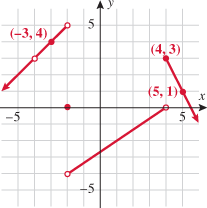
If a vertical line does not intersect the graph of an equation, then that equation does not represent a function. |
| 128.�� | If a horizontal line intersects a graph of an equation more than once, the equation does not represent a function. |
| 129.�� |
If 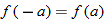 , then , then 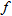 does not represent a function. does not represent a function. |
| 130.�� | If 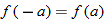 , then , then 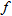 may or may not represent a function. may or may not represent a function. |
| 131.�� |
If 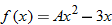 and and 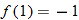 , find , find  . . |
| 132.�� | If 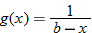 and and 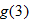 is undefined, find is undefined, find 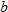 . . |
| CHALLENGE |
| 133.�� |
If
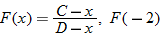 is undefined, and is undefined, and 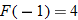 , find , find 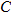 and and  . . |
| 134.�� | Construct a function that is undefined at
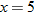 and whose graph passes through the point and whose graph passes through the point 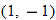 . . |
| 135.�� |
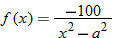 |
| 136.�� | 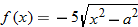 |
| TECHNOLOGY |
| 137.�� |
Using a graphing utility, graph the temperature function in Exercise 103. What time of day is it the warmest? What is the temperature? Looking at this function, explain why this model for Tampa, Florida, is valid only from sunrise to sunset (6 to 18).
|
| 138.�� | Using a graphing utility, graph the height of the firecracker in Exercise 104. How long after liftoff is the firecracker airborne? What is the maximum height that the firecracker attains? Explain why this height model is valid only for the first 8 seconds.
|
| 139.�� |
| 140.�� | The makers of malted milk balls are considering increasing the size of the spherical treats. The thin chocolate coating on a malted milk ball can be approximated by the surface area,
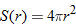 . If the radius is increased 3 mm, what is the resulting increase in required chocolate for the thin outer coating? . If the radius is increased 3 mm, what is the resulting increase in required chocolate for the thin outer coating? |
| 141.�� |
Let
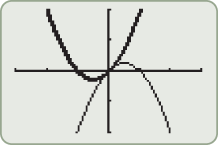
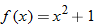 . Graph . Graph 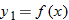 and and 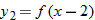 in the same viewing window. Describe how the graph of in the same viewing window. Describe how the graph of 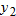 can be obtained from the graph of can be obtained from the graph of 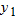 . . |
| 142.�� | Let
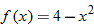 . Graph . Graph 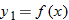 and and 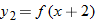 in the same viewing window. Describe how the graph of in the same viewing window. Describe how the graph of  can be obtained from the graph of can be obtained from the graph of  . . |

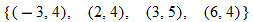

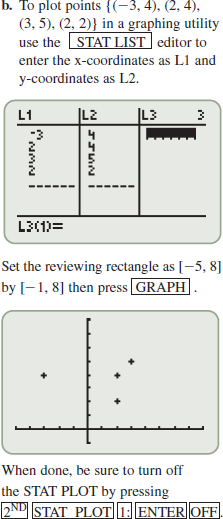
 �Technology Tip
�Technology Tip
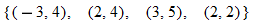
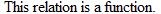
 corresponds to
corresponds to 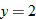 and
and 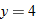 .
. 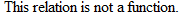
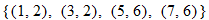

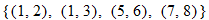
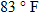 ), (2:00
), (2:00 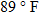 ), (6:00
), (6:00 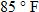 )}
)}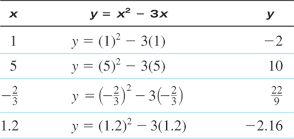
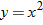
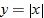
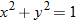
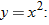
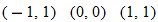
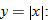
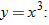
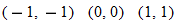
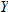
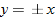
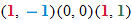
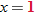 maps to
maps to 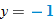 and
and 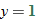
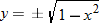
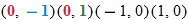
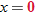 maps to
maps to 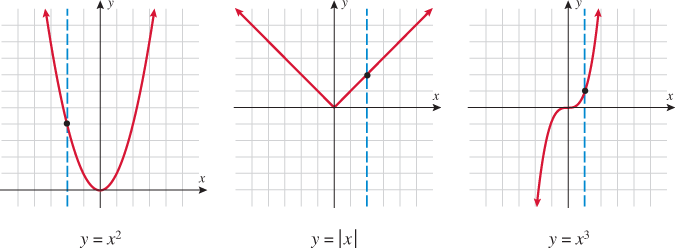

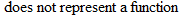 .
.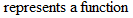 .
.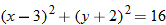 is a function of
is a function of 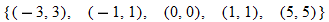
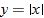
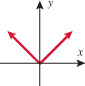
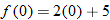
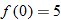
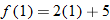
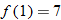
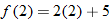
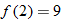
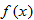 does not mean
does not mean 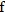 ”. Other common function names are
”. Other common function names are 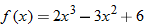 , find
, find 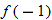 .
.
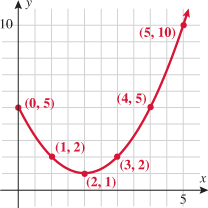
 .
.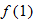 .
. .
.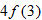 .
.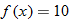 .
.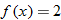 .
. corresponds to the value
corresponds to the value 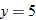 .
. 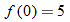
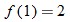
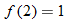
 corresponds to the value
corresponds to the value 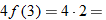
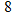
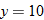 corresponds to the value
corresponds to the value 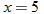 .
.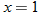 and
and 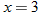 .
.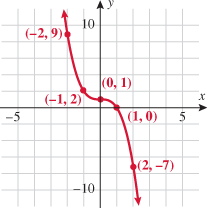
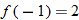
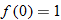
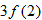
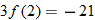
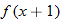 and simplify if possible.
and simplify if possible.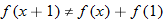 .
.

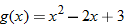 , evaluate
, evaluate 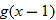 .
.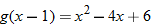
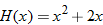 , evaluate:
, evaluate:
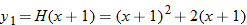 and
and 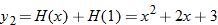 .
.

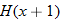
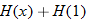
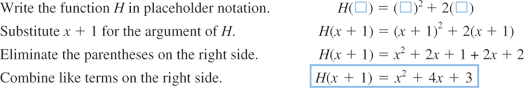
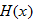 .
.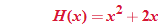
 at
at 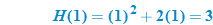
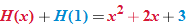
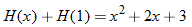
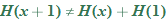 .
.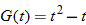 , evaluate:
, evaluate:
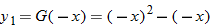 and
and 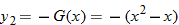 .
.
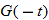
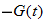
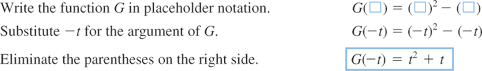
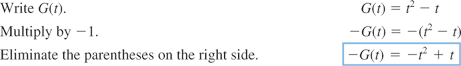
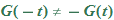 .
.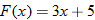 , evaluate:
, evaluate: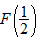
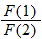
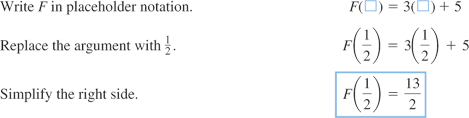
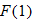 .
.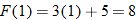
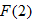 .
.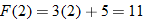
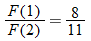
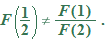
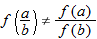
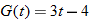 , evaluate:
, evaluate: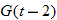
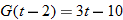
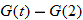
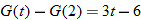
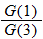
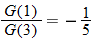
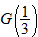
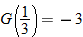
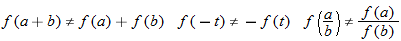
 , find
, find 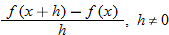 .
.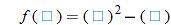
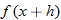 .
.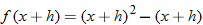
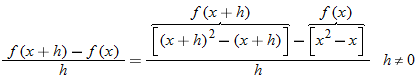
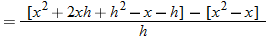
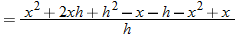
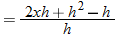
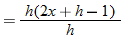
 .
.
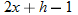

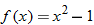 .
.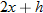
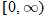
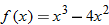
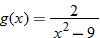
 or
or 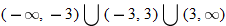
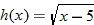
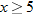 or
or 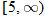
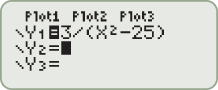
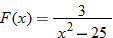 is shown.
is shown.
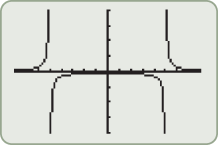
 and 5.
and 5.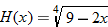
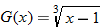
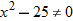
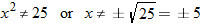

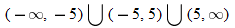
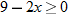
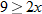
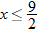
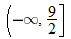
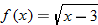
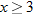 or
or 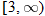
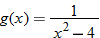
 or
or 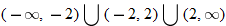
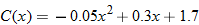 , where
, where 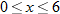 or
or 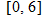 .
.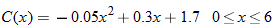
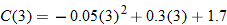
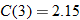
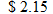 .
.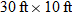 rectangular swimming pool as a function of its depth.
rectangular swimming pool as a function of its depth. , where
, where  is the length,
is the length,  is the width, and
is the width, and 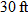 , the width is
, the width is 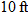 , and the height represents the depth
, and the height represents the depth  of the pool.
of the pool.
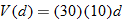
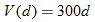
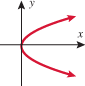
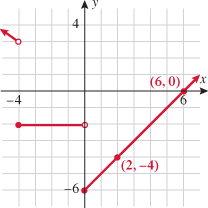
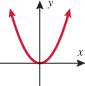 Passes vertical line test
Passes vertical line test , and the
, and the 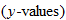 . Placeholder notation is useful when evaluating functions.
. Placeholder notation is useful when evaluating functions.
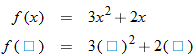
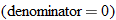 .
.


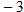 and 3.
and 3.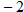 and 2, and 9 maps to both
and 2, and 9 maps to both 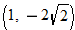 and
and 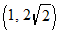 are both on the graph, it does not pass vertical line test.
are both on the graph, it does not pass vertical line test.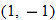 and
and 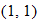 are both on the graph, it does not pass the vertical line test.
are both on the graph, it does not pass the vertical line test.
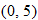 and
and 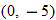 are both on the graph, it does not pass the vertical line test.
are both on the graph, it does not pass the vertical line test.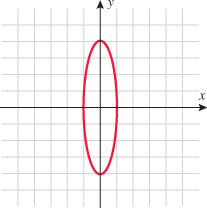
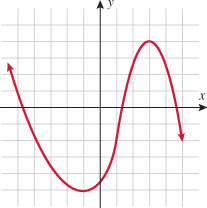
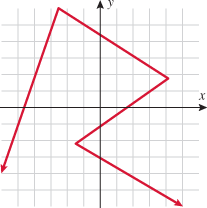
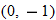 and
and 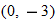 are both on the graph, it does not pass the vertical line test.
are both on the graph, it does not pass the vertical line test.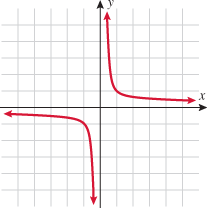

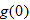
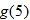
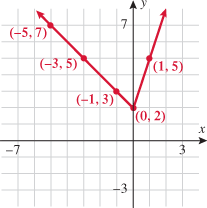
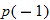
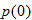
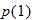
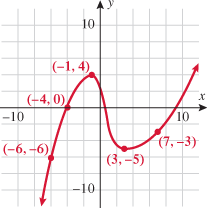
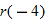
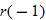
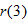
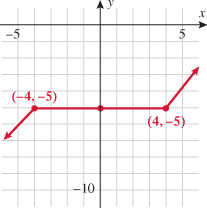
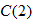
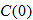
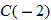
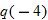
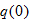
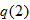
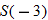
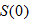
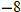
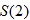
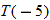
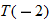
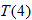
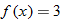 in Exercise
in Exercise 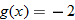 in Exercise
in Exercise 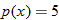 in Exercise
in Exercise 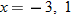
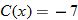 in Exercise
in Exercise 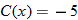 in Exercise
in Exercise 
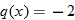 in Exercise
in Exercise 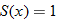 in Exercise
in Exercise 
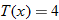 in Exercise
in Exercise 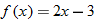
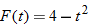
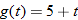
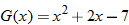
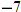
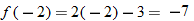
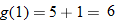

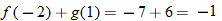 .
.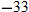
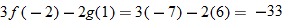 .
.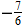
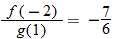 .
.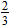
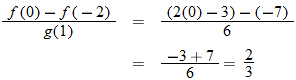
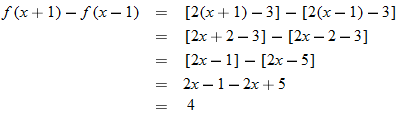
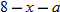
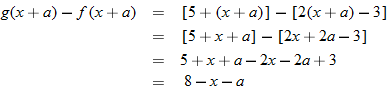
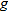 given for Exercises
given for Exercises 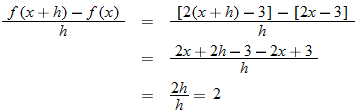
 that this equals
that this equals 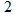 .
. that this equals
that this equals  .
.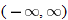
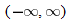 .
.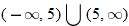
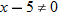 , that is
, that is 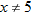 . This is written using interval notation as
. This is written using interval notation as 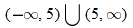 .
.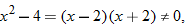
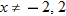 . This is written using interval notation as
. This is written using interval notation as 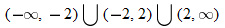 .
.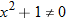 , for every real number
, for every real number 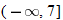
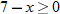 , that is
, that is 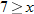 . This is written using interval notation as
. This is written using interval notation as 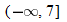 .
.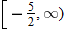
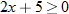 , that is
, that is 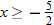 . This is written using interval notation as
. This is written using interval notation as 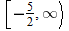 .
.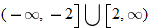
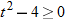 , which is equivalent to
, which is equivalent to 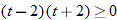 . CPs are
. CPs are 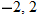

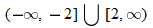 .
.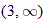
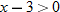 , that is
, that is 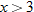 . This is written using interval notation as
. This is written using interval notation as 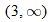 .
.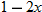 can be any real number, there is no restriction on
can be any real number, there is no restriction on 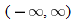 .
.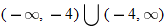
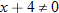 , so that
, so that 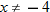 . So, the domain is
. So, the domain is 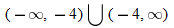 .
.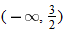
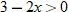 , that is
, that is 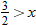 . This is written using interval notation as
. This is written using interval notation as 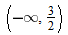 .
.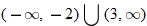
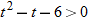 , which is equivalent to
, which is equivalent to 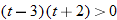 . CPs are
. CPs are 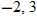

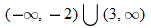 .
.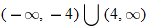
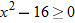 , which is equivalent to
, which is equivalent to 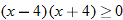 . CPs are
. CPs are 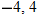

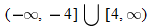 .
.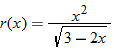 . So, the domain is the set of real numbers
. So, the domain is the set of real numbers 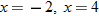
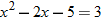 .
.
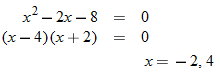
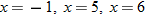
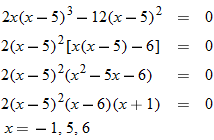
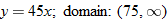
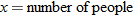 and
and 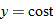 . Then,
. Then, 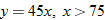 . The domain is
. The domain is 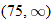 .
.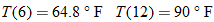
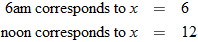
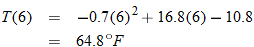
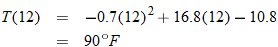
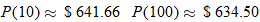
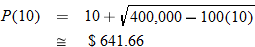
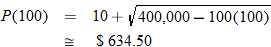
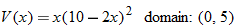
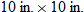 . Then, cut out 4 square corners with dimensions
. Then, cut out 4 square corners with dimensions 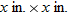 , as shown in the diagram:
, as shown in the diagram:
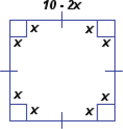
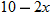 . The volume of the box,
. The volume of the box, 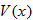 , is given by:
, is given by:
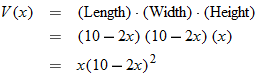
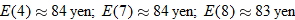
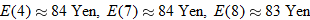
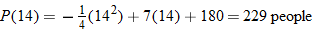
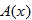 that represents the area of the window in square inches. Simplify, if possible.
that represents the area of the window in square inches. Simplify, if possible.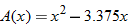
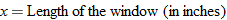
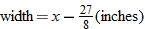
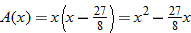 .
.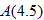 and explain what this value represents.
and explain what this value represents.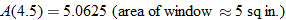
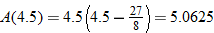 . This means that the area of the window is approximately 5 square inches.
. This means that the area of the window is approximately 5 square inches.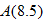 . Is this possible for this particular envelope? Explain.
. Is this possible for this particular envelope? Explain.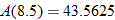 not possible because the window cannot be larger than the envelope.
not possible because the window cannot be larger than the envelope.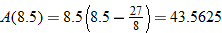 . This would be the area of the window in the envelope. However, this is not possible for an envelope with dimensions 4 inches by 8 inches because the window would be larger than the entire envelope.
. This would be the area of the window in the envelope. However, this is not possible for an envelope with dimensions 4 inches by 8 inches because the window would be larger than the entire envelope.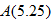 and explain what this value represents.
and explain what this value represents.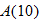 . Is this possible for this particular envelope? Explain.
. Is this possible for this particular envelope? Explain.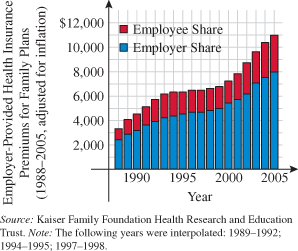
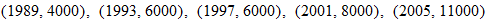
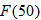
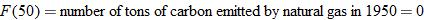
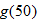
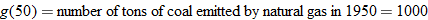
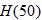
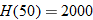
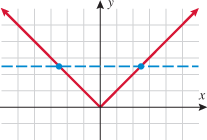
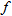 through the input at which you are evaluating it.
through the input at which you are evaluating it.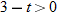
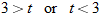
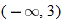
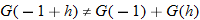
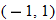 must satisfy the function.
must satisfy the function.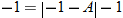
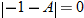
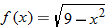 on its domain
on its domain 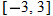 . The vertical line test
. The vertical line test 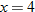 doesn't intersect the graph, but it still defines a function.
doesn't intersect the graph, but it still defines a function.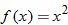 on
on 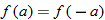 , for all real numbers
, for all real numbers  .
.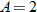
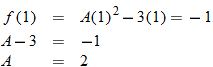
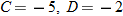
 is undefined only if
is undefined only if 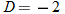 . So,
. So, 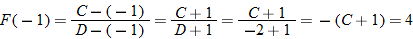 implies that
implies that 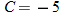 .
.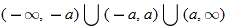
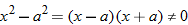 , which is equivalent to
, which is equivalent to 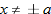 . So, the domain is
. So, the domain is 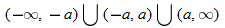 .
.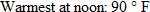 . Outside the interval
. Outside the interval 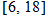 the temperatures are too low.
the temperatures are too low.
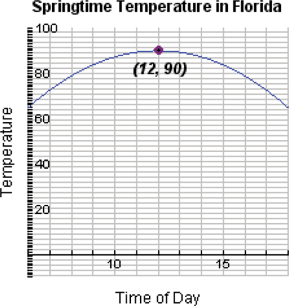
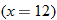 and the temperature is approximately 90 degrees.
and the temperature is approximately 90 degrees.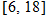 since the values of
since the values of  , highest
, highest 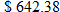 agrees. (If there is only 1 card for sale.)
agrees. (If there is only 1 card for sale.)

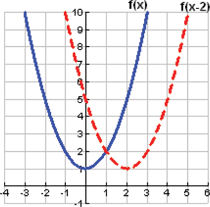
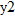 can be obtained by shifting the graph of
can be obtained by shifting the graph of 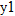 two units to the right.
two units to the right.