Forces and Newton's Laws of Motion

Example�

11�

The Physics of Traction for the Foot

Figure 4.27a shows a traction device used with a foot injury. The weight of the 2.2-kg object creates a tension in the rope that passes around the pulleys. Therefore, tension forces

and

are applied to the pulley on the foot. (It may seem surprising that the rope applies a force to either side of the foot pulley. A similar effect occurs when you place a finger inside a rubber band and push downward. You can feel each side of the rubber band pulling upward on the finger.) The foot pulley is kept in equilibrium because the foot also applies a force

to it. This force arises in reaction (Newton's third law) to the pulling effect of the forces

and

. Ignoring the weight of the foot, find the magnitude of

Figure�4.27�
(a) A traction device for the foot. (b) The free-body diagram for the pulley on the foot.

Reasoning

The forces

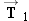
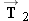
, and

keep the pulley on the foot at rest. The pulley, therefore, has no acceleration and is in equilibrium. As a result, the sum of the x components and the sum of the y components of the three forces must each be zero. Figure 4.27b shows the free-body diagram of the pulley on the foot. The x axis is chosen to be along the direction of force

, and the components of the forces

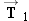
and

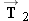
are indicated in the drawing. (See Section 1.7 for a review of vector components.)

Problem-Solving Insight.�

Choose the orientation of the x, y axes for convenience. In Example 11, the axes have been rotated so the force

points along the x axis. Since

does not have a component along the y axis, the analysis is simplified.

Solution

Since the sum of the y components of the forces is zero, it follows that

��(4.9b)

. In other words, the magnitudes of the tension forces are equal. In addition, the sum of the x components of the forces is zero, so we have that

��(4.9a)

Solving for F and letting

, we find that

. However, the tension T in the rope is determined by the weight of the 2.2-kg object:

, where m is its mass and g is the acceleration due to gravity. Therefore, the magnitude of