| Example� |
9� |
The Force Needed to Start a Skier Moving |
|
|
A skier is standing motionless on a horizontal patch of snow. She is holding onto a horizontal tow rope, which is about to pull her forward (see Figure 4.22a). The skier's mass is 59 kg, and the coefficient of static friction between the skis and snow is 0.14. What is the magnitude of the maximum force that the tow rope can apply to the skier without causing her to move?
Reasoning
When the rope applies a relatively small force, the skier does not accelerate. The reason is that the static frictional force opposes the applied force and the two forces have the same magnitude. We can apply Newton's second law in the horizontal direction to this situation. In order for the rope to pull the skier forward, it must exert a force large enough to overcome the maximum static frictional force acting on the skis. The magnitude of the maximum static frictional force depends on the coefficient of static friction (which is known) and on the magnitude of the normal force. We can determine the magnitude of the normal force by using Newton's second law, along with the fact that the skier does not accelerate in the vertical direction.
Knowns and Unknowns The data for this problem are as follows:
Description |
Symbol |
Value |
Mass of skier |
m |
59 kg |
Coefficient of static friction |
|
0.14 |
Unknown Variable |
� |
� |
Magnitude of maximum horizontal force that tow rope can apply |
F |
? |
|
|
Modeling the Problem
 Newton's Second Law (Horizontal Direction) Figure 4.22 a shows the two horizontal forces that act on the skier just before she begins to move: the force 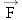 applied by the tow rope and the maximum static frictional force  . Since the skier is standing motionless, she is not accelerating in the horizontal or x direction, so 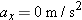 . Applying Newton's second law (Equation 4.2a) to this situation, we have
Since the net force  in the x direction is  , Newton's second law can be written as  . Thus,
We do not know 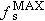 , but its value will be determined in Steps 2 and 3. |
|
 The Maximum Static Frictional Force The magnitude 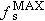of the maximum static frictional force is related to the coefficient of static friction 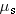 and the magnitude 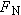 of the normal force by Equation 4.7:
We now substitute this result into Equation 1, as indicated in the right column. The coefficient of static friction is known, but 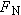is not. An expression for 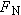will be obtained in the next step. |
|
 Newton's Second Law (Vertical Direction) We can find the magnitude 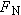of the normal force by noting that the skier does not accelerate in the vertical or y direction, so 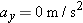 . Figure 4.22 b shows the two vertical forces that act on the skier: the normal force 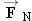 and her weight  . Applying Newton's second law (Equation 4.2b) in the vertical direction gives
The net force in the y direction is  , so Newton's second law becomes  . Thus,
We now substitute this result into Equation 4.7, as shown at the right. |
|
|
|
Solution
Algebraically combining the results of the three steps, we have
The magnitude F of the maximum force is
If the force exerted by the tow rope exceeds this value, the skier will begin to accelerate forward.
|
|
|
|
