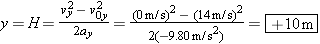|
A placekicker kicks a football at an angle of 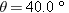 above the horizontal axis, as Figure 3.12 shows. The initial speed of the ball is above the horizontal axis, as Figure 3.12 shows. The initial speed of the ball is 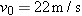 . Ignore air resistance and find the maximum height H that the ball attains. . Ignore air resistance and find the maximum height H that the ball attains.
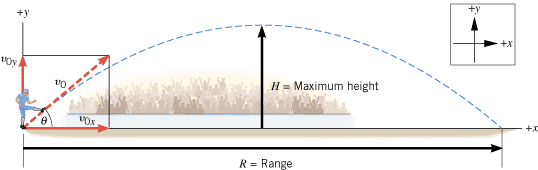 | | Figure 3.12
A football is kicked with an initial speed of v0 at an angle of q above the ground. The ball attains a maximum height H and a range R. |
|
Reasoning
The maximum height is a characteristic of the vertical part of the motion, which can be treated separately from the horizontal part. In preparation for making use of this fact, we calculate the vertical component of the initial velocity:
The vertical component of the velocity, vy, decreases as the ball moves upward. Eventually, vy = = 0 m/s at the maximum height H. The data below can be used in Equation 3.6b ( 0 m/s at the maximum height H. The data below can be used in Equation 3.6b (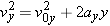 ) to find the maximum height: ) to find the maximum height:
y-Direction Data
|
y
|
ay
|
vy
|
v0y
|
t
|
H = = ? ?
|
–9.80 m/s2
|
0 m/s
|
+14 m/s
|
?
|
Problem solving insight
When a projectile reaches maximum height, the vertical component of its velocity is momentarily zero (vy = = 0 m/s). However, the horizontal component of its velocity is not zero. 0 m/s). However, the horizontal component of its velocity is not zero. |
|
Solution
From Equation 3.6b, we find that
The height H depends only on the y variables; the same height would have been reached had the ball been thrown straight up with an initial velocity of v0y = = +14 m/s. +14 m/s.
|
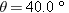 above the horizontal axis, as Figure 3.12 shows. The initial speed of the ball is
above the horizontal axis, as Figure 3.12 shows. The initial speed of the ball is 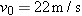 . Ignore air resistance and find the maximum height H that the ball attains.
. Ignore air resistance and find the maximum height H that the ball attains.
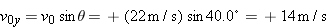
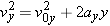 ) to find the maximum height:
) to find the maximum height: