2.6.
Freely Falling Bodies
Everyone has observed the effect of gravity as it causes objects to fall downward. In the absence of air resistance, it is found that all bodies at the same location above the earth fall vertically with the same acceleration. Furthermore, if the distance of the fall is small compared to the radius of the earth, the acceleration remains essentially constant throughout the descent. This idealized motion, in which air resistance is neglected and the acceleration is nearly constant, is known as free-fall. Since the acceleration is constant in free-fall, the equations of kinematics can be used.
The acceleration of a freely falling body is called the acceleration due to gravity, and its magnitude (without any algebraic sign) is denoted by the symbol g. The acceleration due to gravity is directed downward, toward the center of the earth. Near the earth’s surface, g is approximately
Unless circumstances warrant otherwise, we will use either of these values for g in subsequent calculations. In reality, however, g decreases with increasing altitude and varies slightly with latitude.
Figure 2.16a shows the well-known phenomenon of a rock falling faster than a sheet of paper. The effect of air resistance is responsible for the slower fall of the paper, for when air is removed from the tube, as in Figure 2.16b, the rock and the paper have exactly the same acceleration due to gravity. In the absence of air, the rock and the paper both exhibit free-fall motion. Free-fall is closely approximated for objects falling near the surface of the moon, where there is no air to retard the motion. A nice demonstration of lunar free-fall was performed by astronaut David Scott, who dropped a hammer and a feather simultaneously from the same height. Both experienced the same acceleration due to lunar gravity and consequently hit the ground at the same time. The acceleration due to gravity near the surface of the moon is approximately one-sixth as large as that on the earth.
 | | Figure 2.16
(a) In the presence of air resistance, the acceleration of the rock is greater than that of the paper. (b) In the absence of air resistance, both the rock and the paper have the same acceleration. |
|
When the equations of kinematics are applied to free-fall motion, it is natural to use the symbol y for the displacement, since the motion occurs in the vertical or y direction. Thus, when using the equations in Table 2.1 for free-fall motion, we will simply replace x with y. There is no significance to this change. The equations have the same algebraic form for either the horizontal or vertical direction, provided that the acceleration remains constant during the motion. We now turn our attention to several examples that illustrate how the equations of kinematics are applied to freely falling bodies.
| Example 10 A Falling Stone |
 |
|
A stone is dropped from rest from the top of a tall building, as Figure 2.17 indicates. After 3.00 s of free-fall, what is the displacement y of the stone?
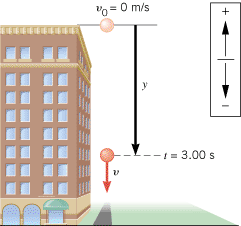 | | Figure 2.17
The stone, starting with zero velocity at the top of the building, is accelerated downward by gravity. |
|
Reasoning
The upward direction is chosen as the positive direction. The three known variables are shown in the box below. The initial velocity v0 of the stone is zero, because the stone is dropped from rest. The acceleration due to gravity is negative, since it points downward in the negative direction.
Stone Data
|
y
|
a
|
v
|
v0
|
t
|
?
|
–9.80 m/s2
|
|
0 m/s
|
3.00 s
|
Equation 2.8 contains the appropriate variables and offers a direct solution to the problem. Since the stone moves downward, and upward is the positive direction, we expect the displacement y to have a negative value.
Solution
Using Equation 2.8, we find that
The answer for y is negative, as expected.
|
 |
| Example 11 The Velocity of a Falling Stone |
 |
|
After 3.00 s of free-fall, what is the velocity v of the stone in Figure 2.17?
Reasoning
Because of the acceleration due to gravity, the magnitude of the stone’s downward velocity increases by 9.80 m/s during each second of free-fall. The data for the stone are the same as in Example 10, and Equation 2.4 offers a direct solution for the final velocity. Since the stone is moving downward in the negative direction, the value determined for v should be negative.
Solution
Using Equation 2.4, we obtain
The velocity is negative, as expected.
|
 |
The acceleration due to gravity is always a downward-pointing vector. It describes how the speed increases for an object that is falling freely downward. This same acceleration also describes how the speed decreases for an object moving upward under the influence of gravity alone, in which case the object eventually comes to a momentary halt and then falls back to earth. Examples 12 and 13 show how the equations of kinematics are applied to an object that is moving upward under the influence of gravity.
Problem solving insight
“Implied data” are important. In Example 12, for instance, the phrase “how high does the coin go” refers to the maximum height, which occurs when the final velocity v in the vertical direction is v = = 0 m/s. 0 m/s. |
|
| Example 12 How High Does It Go? |
| Example 13 How Long Is It in the Air? |
 |
|
In Figure 2.18, what is the total time the coin is in the air before returning to its release point?
Reasoning
During the time the coin travels upward, gravity causes its speed to decrease to zero. On the way down, however, gravity causes the coin to regain the lost speed. Thus, the time for the coin to go up is equal to the time for it to come down. In other words, the total travel time is twice the time for the upward motion. The data for the coin during the upward trip are the same as in Example 12. With these data, we can use Equation 2.4 (v = = v0 v0 + + at) to find the upward travel time. at) to find the upward travel time.
Solution
Rearranging Equation 2.4 , we find that
The total up-and-down time is twice this value, or  .
It is possible to determine the total time by another method. When the coin is tossed upward and returns to its release point, the displacement for the entire trip is y .
It is possible to determine the total time by another method. When the coin is tossed upward and returns to its release point, the displacement for the entire trip is y = = 0 m. With this value for the displacement, Equation 2.8 0 m. With this value for the displacement, Equation 2.8  can be used to find the time for the entire trip directly. can be used to find the time for the entire trip directly.
|
 |
Examples 12 and 13 illustrate that the expression “freely falling” does not necessarily mean an object is falling down. A freely falling object is any object moving either upward or downward under the influence of gravity alone. In either case, the object always experiences the same downward acceleration due to gravity, a fact that is the focus of the next example.
| Conceptual Example 14 Acceleration Versus Velocity |
 |
|
There are three parts to the motion of the coin in Figure 2.18. On the way up, the coin has a velocity vector that is directed upward and has a decreasing magnitude. At the top of its path, the coin momentarily has a zero velocity. On the way down, the coin has a downward-pointing velocity vector with an increasing magnitude. In the absence of air resistance, does the acceleration of the coin, like the velocity, change from one part of the motion to another?
Reasoning and Solution Since air resistance is absent, the coin is in free-fall motion. Therefore, the acceleration vector is that due to gravity and has the same magnitude and the same direction at all times. It has a magnitude of 9.80 m/s2 and points downward during both the upward and downward portions of the motion. Furthermore, just because the coin’s instantaneous velocity is zero at the top of the motional path, don’t think that the acceleration vector is also zero there. Acceleration is the rate at which velocity changes, and the velocity at the top is changing, even though at one instant it is zero. In fact, the acceleration at the top has the same magnitude of 9.80 m/s2 and the same downward direction as during the rest of the motion. Thus, the coin’s velocity vector changes from moment to moment, but its acceleration vector does not change.
|
 |
The motion of an object that is thrown upward and eventually returns to earth contains a symmetry that is useful to keep in mind from the point of view of problem solving. The calculations just completed indicate that a time symmetry exists in free-fall motion, in the sense that the time required for the object to reach maximum height equals the time for it to return to its starting point.
A type of symmetry involving the speed also exists. Figure 2.19 shows the coin considered in Examples 12 and 13. At any displacement y above the point of release, the coin’s speed during the upward trip equals the speed at the same point during the downward trip. For instance, when y =
= +1.04 m, Equation 2.9 gives two possible values for the final velocity v, assuming that the initial velocity is v0
+1.04 m, Equation 2.9 gives two possible values for the final velocity v, assuming that the initial velocity is v0 =
= +5.00 m/s:
+5.00 m/s:
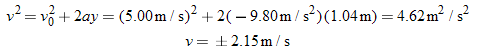 |  |
The value v =
= +2.15 m/s is the velocity of the coin on the upward trip, and v
+2.15 m/s is the velocity of the coin on the upward trip, and v =
= –2.15 m/s is the velocity on the downward trip. The speed in both cases is identical and equals 2.15 m/s. Likewise, the speed just as the coin returns to its point of release is 5.00 m/s, which equals the initial speed. This symmetry involving the speed arises because the coin loses 9.80 m/s in speed each second on the way up and gains back the same amount each second on the way down. In Conceptual Example 15, we use just this kind of symmetry to guide our reasoning as we analyze the motion of a pellet shot from a gun.
–2.15 m/s is the velocity on the downward trip. The speed in both cases is identical and equals 2.15 m/s. Likewise, the speed just as the coin returns to its point of release is 5.00 m/s, which equals the initial speed. This symmetry involving the speed arises because the coin loses 9.80 m/s in speed each second on the way up and gains back the same amount each second on the way down. In Conceptual Example 15, we use just this kind of symmetry to guide our reasoning as we analyze the motion of a pellet shot from a gun.
 Concept Simulation 2.3 Concept Simulation 2.3 |
 |
In Figure 2.19 changing the initial velocity affects how high the coin goes and its total flight time. Here you can change the initial velocity and see how the motion of the coin changes. Related Homework: Conceptual Question 13, Problems 39, 42, 50, 86 |
|
 |
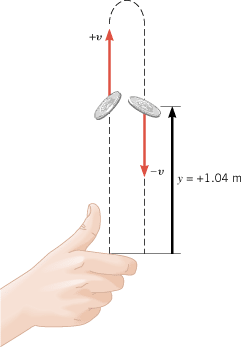 | | Figure 2.19
For a given displacement along the motional path, the upward speed of the coin is equal to its downward speed, but the two velocities point in opposite directions. |
|
| Conceptual Example 15 Taking Advantage of Symmetry |
 |
|
Figure 2.20a shows a pellet, having been fired from a gun, moving straight upward from the edge of a cliff. The initial speed of the pellet is 30 m/s. It goes up and then falls back down, eventually hitting the ground beneath the cliff. In Figure 2.20b the pellet has been fired straight downward at the same initial speed. In the absence of air resistance, does the pellet in part b strike the ground beneath the cliff with a smaller, a greater, or the same speed as the pellet in part a?
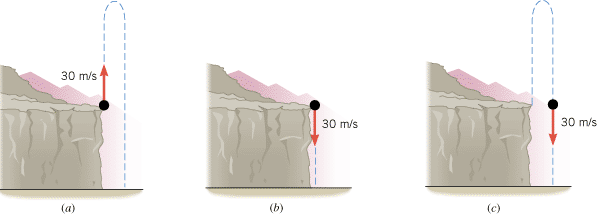 | | Figure 2.20
(a) From the edge of a cliff, a pellet is fired straight upward from a gun. The pellet’s initial speed is 30 m/s. (b) The pellet is fired straight downward with an initial speed of 30 m/s. (c) In Conceptual Example 15 this drawing plays the central role in reasoning that is based on symmetry. |
|
Reasoning and Solution Because air resistance is absent, the motion is that of free-fall, and the symmetry inherent in free-fall motion offers an immediate answer to the question. Figure 2.20c shows why. This part of the drawing shows the pellet after it has been fired upward and then fallen back down to its starting point. Symmetry indicates that the speed in part c is the same as in part a — — namely, 30 m/s. Thus, part c is just like part b, where the pellet is actually fired downward with a speed of 30 m/s. Consequently, whether the pellet is fired as in part a or part b, it starts to move downward from the cliff edge at a speed of 30 m/s. In either case, there is the same acceleration due to gravity and the same displacement from the cliff edge to the ground below. Under these conditions, the pellet reaches the ground with the same speed no matter in which vertical direction it is fired initially. namely, 30 m/s. Thus, part c is just like part b, where the pellet is actually fired downward with a speed of 30 m/s. Consequently, whether the pellet is fired as in part a or part b, it starts to move downward from the cliff edge at a speed of 30 m/s. In either case, there is the same acceleration due to gravity and the same displacement from the cliff edge to the ground below. Under these conditions, the pellet reaches the ground with the same speed no matter in which vertical direction it is fired initially.
Related Homework:
Problems 43
, 46
|
 |
| Check Your Understanding 4 |
 |
|
A ball is thrown straight upward with a velocity v0 and in a time t reaches the top of its flight path, which is a displacement y above the launch point. With a launch velocity of 2v0, what would be the time required to reach the top of its flight path and what would be the displacement of the top point above the launch point?
| (a) |
4t and 2y
| | (b) |
2t and 4y
| | (c) |
2t and 2y
| | (d) |
4t and 4y
| | (e) |
t and 2y
|
Background:
The acceleration due to gravity and the equations of kinematics given in Table 2.1 are the focus of this question.
For similar questions (including calculational counterparts), consult Self-Assessment Test 2.3. This test is described at the end of Section 2.7.
|
|
 |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |



 .
It is possible to determine the total time by another method. When the coin is tossed upward and returns to its release point, the displacement for the entire trip is y
.
It is possible to determine the total time by another method. When the coin is tossed upward and returns to its release point, the displacement for the entire trip is y can be used to find the time for the entire trip directly.
can be used to find the time for the entire trip directly.
![]() =
=![]() +1.04 m, Equation 2.9 gives two possible values for the final velocity v, assuming that the initial velocity is v0
+1.04 m, Equation 2.9 gives two possible values for the final velocity v, assuming that the initial velocity is v0![]() =
=![]() +5.00 m/s:
+5.00 m/s: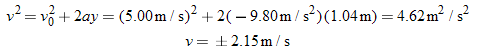
![]() =
=![]() +2.15 m/s is the velocity of the coin on the upward trip, and v
+2.15 m/s is the velocity of the coin on the upward trip, and v![]() =
=![]() –2.15 m/s is the velocity on the downward trip. The speed in both cases is identical and equals 2.15 m/s. Likewise, the speed just as the coin returns to its point of release is 5.00 m/s, which equals the initial speed. This symmetry involving the speed arises because the coin loses 9.80 m/s in speed each second on the way up and gains back the same amount each second on the way down. In Conceptual Example 15, we use just this kind of symmetry to guide our reasoning as we analyze the motion of a pellet shot from a gun.
–2.15 m/s is the velocity on the downward trip. The speed in both cases is identical and equals 2.15 m/s. Likewise, the speed just as the coin returns to its point of release is 5.00 m/s, which equals the initial speed. This symmetry involving the speed arises because the coin loses 9.80 m/s in speed each second on the way up and gains back the same amount each second on the way down. In Conceptual Example 15, we use just this kind of symmetry to guide our reasoning as we analyze the motion of a pellet shot from a gun. Concept Simulation 2.3
Concept Simulation 2.3