3.3.
Projectile Motion
The biggest thrill in baseball is a home run. The motion of the ball on its curving path into the stands is a common type of two-dimensional motion called “projectile motion.” A good description of such motion can often be obtained with the assumption that air resistance is absent.
 CONCEPTS AT A GLANCE Following the approach outlined in Figure 3.6, we consider the horizontal and vertical parts of the motion separately. In the horizontal or x direction, the moving object (the projectile) does not slow down in the absence of air resistance. Thus, the x component of the velocity remains constant at its initial value or vx
CONCEPTS AT A GLANCE Following the approach outlined in Figure 3.6, we consider the horizontal and vertical parts of the motion separately. In the horizontal or x direction, the moving object (the projectile) does not slow down in the absence of air resistance. Thus, the x component of the velocity remains constant at its initial value or vx =
= v0x, and the x component of the acceleration is ax
v0x, and the x component of the acceleration is ax =
= 0 m/s2. In the vertical or y direction, however, the projectile experiences the effect of gravity. As a result, the y component of the velocity vy is not constant, but changes. The y component of the acceleration ay is the downward acceleration due to gravity. If the path or trajectory of the projectile is near the earth’s surface, ay has a magnitude of 9.80 m/s2. In this text, then, the phrase “projectile motion” means that ax
0 m/s2. In the vertical or y direction, however, the projectile experiences the effect of gravity. As a result, the y component of the velocity vy is not constant, but changes. The y component of the acceleration ay is the downward acceleration due to gravity. If the path or trajectory of the projectile is near the earth’s surface, ay has a magnitude of 9.80 m/s2. In this text, then, the phrase “projectile motion” means that ax =
= 0 m/s2 and ay equals the acceleration due to gravity, as the Concept-at-a-Glance chart in Figure 3.8 summarizes. Example 2 and other examples in this section illustrate how the equations of kinematics are applied to projectile motion.
0 m/s2 and ay equals the acceleration due to gravity, as the Concept-at-a-Glance chart in Figure 3.8 summarizes. Example 2 and other examples in this section illustrate how the equations of kinematics are applied to projectile motion.
|
| Figure 3.8
CONCEPTS AT A GLANCEIn projectile motion, the horizontal or x component of the acceleration is zero, and the vertical or y component of the acceleration is the acceleration due to gravity. In this time-lapse photograph, the cat exhibits projectile motion while in the air, assuming that the effects of air resistance can be ignored. (© Stephen Dalton/Photo Researchers). |
|
| Example 2 A Falling Care Package |
 |
|
Figure 3.9 shows an airplane moving horizontally with a constant velocity of +115 m/s at an altitude of 1050 m. The directions to the right and upward have been chosen as the positive directions. The plane releases a “care package” that falls to the ground along a curved trajectory. Ignoring air resistance, determine the time required for the package to hit the ground.
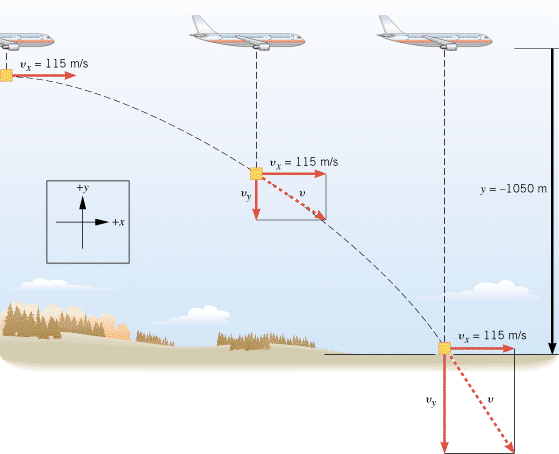 | | Figure 3.9
The package falling from the plane is an example of projectile motion, as Examples 2 and 3 discuss. |
|
Reasoning
The time required for the package to hit the ground is the time it takes for the package to fall through a vertical distance of 1050 m. In falling, it moves to the right, as well as downward, but these two parts of the motion occur independently. Therefore, we can focus solely on the vertical part. We note that the package is moving initially in the horizontal or x direction, not in the y direction, so that v0y = = 0 m/s. Furthermore, when the package hits the ground, the y component of its displacement is y 0 m/s. Furthermore, when the package hits the ground, the y component of its displacement is y = = –1050 m, as the drawing shows. The acceleration is that due to gravity, so ay –1050 m, as the drawing shows. The acceleration is that due to gravity, so ay = = –9.80 m/s2. These data are summarized as follows: –9.80 m/s2. These data are summarized as follows:
y-Direction Data
|
y
|
ay
|
vy
|
v0y
|
t
|
–1050 m
|
–9.80 m/s2
|
|
0 m/s
|
?
|
With these data, Equation 3.5b (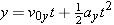 ) can be used to find the fall time. ) can be used to find the fall time.
Problem solving insight
The variables y, ay, vy, and v0y are scalar components. Therefore, an algebraic sign (+ or –) must be included with each one to denote direction. |
|
Solution
Since v0y = = 0 m/s, it follows from Equation 3.5b that 0 m/s, it follows from Equation 3.5b that 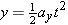 and and
|
 |
The freely falling package in Example 2 picks up vertical speed on the way down. The horizontal component of the velocity, however, retains its initial value of v0x =
= +115 m/s throughout the entire descent. Since the plane also travels at a constant horizontal velocity of +115 m/s, it remains directly above the falling package. The pilot always sees the package directly beneath the plane, as the dashed vertical lines in Figure 3.9 show. This result is a direct consequence of the fact that the package has no acceleration in the horizontal direction. In reality, air resistance would slow down the package, and it would not remain directly beneath the plane during the descent. Figure 3.10 further clarifies this point by illustrating what happens to two packages that are released simultaneously from the same height. Package B is given an initial velocity component of v0x
+115 m/s throughout the entire descent. Since the plane also travels at a constant horizontal velocity of +115 m/s, it remains directly above the falling package. The pilot always sees the package directly beneath the plane, as the dashed vertical lines in Figure 3.9 show. This result is a direct consequence of the fact that the package has no acceleration in the horizontal direction. In reality, air resistance would slow down the package, and it would not remain directly beneath the plane during the descent. Figure 3.10 further clarifies this point by illustrating what happens to two packages that are released simultaneously from the same height. Package B is given an initial velocity component of v0x =
= +115 m/s in the horizontal direction, as in Example 2, and the package follows the path shown in the figure. Package A, on the other hand, is dropped from a stationary balloon and falls straight down toward the ground, since v0x
+115 m/s in the horizontal direction, as in Example 2, and the package follows the path shown in the figure. Package A, on the other hand, is dropped from a stationary balloon and falls straight down toward the ground, since v0x =
= 0 m/s. Both packages hit the ground at the same time.
0 m/s. Both packages hit the ground at the same time.
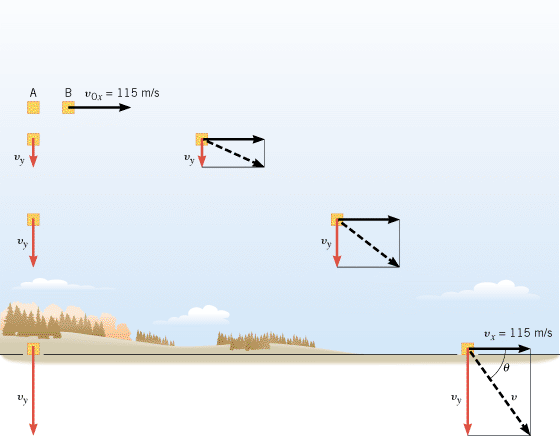 | | Figure 3.10
Package A and package B are released simultaneously at the same height and strike the ground at the same time because their y variables (y, ay, and v0y) are the same. |
|
Not only do the packages in Figure 3.10 reach the ground at the same time, but the y components of their velocities are also equal at all points on the way down. However, package B does hit the ground with a greater speed than does package A. Remember, speed is the magnitude of the velocity vector, and the velocity of B has an x component, whereas the velocity of A does not. The magnitude and direction of the velocity vector for package B at the instant just before the package hits the ground is computed in Example 3.
| Example 3 The Velocity of the Care Package |
 |
|
For the situation shown in Figure 3.10, find the speed of package B and the direction of the velocity vector just before package B hits the ground.
Reasoning
Since the speed v of the package is given by 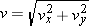 it is necessary to know values for vx and vy at the instant before impact. The component vx is constant and has a value of 115 m/s. The component vy can be determined by using Equation 3.3b and the data from Example 2 (ay it is necessary to know values for vx and vy at the instant before impact. The component vx is constant and has a value of 115 m/s. The component vy can be determined by using Equation 3.3b and the data from Example 2 (ay = = –9.80 m/s2, v0y –9.80 m/s2, v0y = = 0 m/s, t 0 m/s, t = = 14.6 s). Thus, we expect that the final speed v of package B will be greater than 115 m/s. 14.6 s). Thus, we expect that the final speed v of package B will be greater than 115 m/s.
Problem solving insight
The speed of a projectile at any location along its path is the magnitude v of its velocity at that location: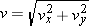 . Both the horizontal and vertical velocity components contribute to the speed. . Both the horizontal and vertical velocity components contribute to the speed. |
|
Solution
From Equation 3.3b, it follows that
The speed of package B at the instant before impact is
which is greater than 115 m/s, as expected. The velocity vector makes an angle q with the horizontal, as Figure 3.10 indicates:
|
 |
An important feature of projectile motion is that there is no acceleration in the horizontal or x direction. Conceptual Example 4 discusses an interesting implication of this feature.
| Conceptual Example 4 I Shot a Bullet into the Air… |
 |
|
Suppose you are driving in a convertible with the top down. The car is moving to the right at a constant velocity. As Figure 3.11 illustrates, you point a rifle straight upward and fire it. In the absence of air resistance, where would the bullet land—behind you, ahead of you, or in the barrel of the rifle?
 | | Figure 3.11
The car is moving with a constant velocity to the right, and the rifle is pointed straight up. In the absence of air resistance, a bullet fired from the rifle has no acceleration in the horizontal direction. As a result, the bullet would land back in the barrel of the rifle. |
|
Reasoning and Solution If air resistance were present, it would slow down the bullet and cause it to land behind you, toward the rear of the car. However, air resistance is absent, so we must consider the bullet’s motion more carefully. Before the rifle is fired, the bullet, rifle, and car are moving together, so the bullet and rifle have the same horizontal velocity as the car. When the rifle is fired, the bullet is given an additional velocity component in the vertical direction; the bullet retains the velocity of the car as its initial horizontal velocity component, since the rifle is pointed straight up. Because there is no air resistance to slow it down, the bullet experiences no horizontal acceleration. Thus, the bullet’s horizontal velocity component does not change. It retains its initial value, and remains matched to that of the rifle and the car. As a result, the bullet remains directly above the rifle at all times and would fall directly back into the barrel of the rifle, as the drawing indicates. This situation is analogous to that in Figure 3.9, where the care package, as it falls, remains directly below the plane.
Related Homework:
Conceptual Question 12, Problem 34
|
 |
 Concept Simulation 3.1 Concept Simulation 3.1 |
 |
In this simulation, which is discussed in Conceptual Example 4 and illustrated in Figure 3.11, you can alter the trajectory of the bullet by changing the speed of the car and the initial speed of the bullet. In addition, the simulation shows the x and y components of the bullet’s velocity as the bullet moves through the air. Related Homework: Conceptual Question 7, Problem 34 |
|
 |
Often projectiles, like footballs and baseballs, are sent into the air at an angle with respect to the ground. From a knowledge of the projectile’s initial velocity, a wealth of information can be obtained about the motion. For instance, Example 5 demonstrates how to calculate the maximum height reached by the projectile.
| Example 5 The Height of a Kickoff |
It is also possible to find the total time or “hang time” during which the football in Figure 3.12 is in the air. Example 6 shows how to determine this time.
| Example 6 The Time of Flight of a Kickoff |
 |
|
For the motion illustrated in Figure 3.12, ignore air resistance and use the data from Example 5 to determine the time of flight between kickoff and landing.
Reasoning
Given the initial velocity, it is the acceleration due to gravity that determines how long the ball stays in the air. Thus, to find the time of flight we deal with the vertical part of the motion. Since the ball starts at and returns to ground level, the displacement in the y direction is zero. The initial velocity component in the y direction is the same as that in Example 5; that is, v0y = = +14 m/s. Therefore, we have +14 m/s. Therefore, we have
y-Direction Data
|
y
|
ay
|
vy
|
v0y
|
t
|
0 m
|
–9.80 m/s2
|
|
+14 m/s
|
?
|
The time of flight can be determined from Equation 3.5b 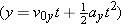
Solution
Using Equation 3.5b, we find
There are two solutions to this equation. One is given by
The other is given by 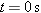 . The solution we seek is . The solution we seek is 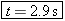 , because , because 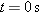 corresponds to the initial kickoff. corresponds to the initial kickoff.
|
 |
Another important feature of projectile motion is called the “range.” The range, as Figure 3.12 shows, is the horizontal distance traveled between launching and landing, assuming the projectile returns to the same vertical level at which it was fired. Example 7 shows how to obtain the range.
 Concept Simulation 3.2 Concept Simulation 3.2 |
 |
This simulation will let you explore projectile motion, along with the concepts of maximum height and range. You can control the initial speed and angle of a ball and then see how its velocity components change with time as it moves along the curved path. The simulation also displays graphs of position and velocity as functions of time. Related Homework: Problems 18, 73 |
|
 |
| Example 7 The Range of a Kickoff |
 |
|
For the motion shown in Figure 3.12 and discussed in Examples 5 and 6, ignore air resistance and calculate the range R of the projectile.
Reasoning
The range is a characteristic of the horizontal part of the motion. Thus, our starting point is to determine the horizontal component of the initial velocity:
Recall from Example 6 that the time of flight is 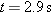 . Since there is no acceleration in the x direction, vx remains constant, and the range is simply the product of . Since there is no acceleration in the x direction, vx remains constant, and the range is simply the product of 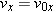 and the time. and the time.
Solution
The range is
|
 |
The range in the previous example depends on the angle q at which the projectile is fired above the horizontal. When air resistance is absent, the maximum range results when 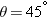 .
.
| Check Your Understanding 3 |
 |
|
A projectile is fired into the air, and it follows the parabolic path shown in the drawing. There is no air resistance. At any instant, the projectile has a velocity v and an acceleration a. Which one or more of the drawings could not represent the directions for v and a at any point on the trajectory?
Background:
The fundamental nature of projectile motion lies at the heart of this question, as does the nature of gravity.
For similar questions (including calculational counterparts), consult Self-Assessment Test 3.1. This test is described at the end of this section.
|
|
 |
The examples considered thus far have used information about the initial location and velocity of a projectile to determine the final location and velocity. Example 8 deals with the opposite situation and illustrates how the final parameters can be used with the equations of kinematics to determine the initial parameters.
 |
|
A baseball player hits a home run, and the ball lands in the left-field seats, 7.5 m above the point at which it was hit. It lands with a velocity of 36 m/s at an angle of 28° below the horizontal (see Figure 3.13). Ignoring air resistance, find the initial velocity with which the ball leaves the bat.
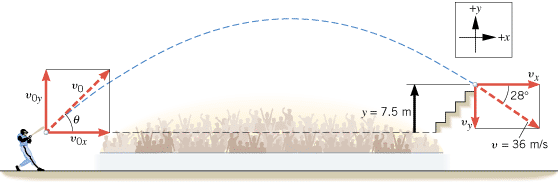 | | Figure 3.13
The velocity and location of the baseball upon landing can be used to determine its initial velocity, as Example 8 illustrates.
|
|
Reasoning
To find the initial velocity, we must determine its magnitude (the initial speed v0) and its direction (the angle q in the drawing). These quantities are related to the horizontal and vertical components of the initial velocity (v0x and v0y) by the relations
Therefore, it is necessary to find v0x and v0y, which we will do with the equations of kinematics.
Solution
Since air resistance is being ignored, the horizontal component of the velocity vxremains constant throughout the motion. Thus,
The value for v0y can be obtained from Equation 3.6b and the data displayed below (see Figure 3.13 for the positive and negative directions):
y-Direction Data
|
y
|
ay
|
vy
|
v0y
|
t
|
+7.5 m
|
–9.80 m/s2
|
(–36 sin 28°) m/s
|
?
|
|
In determining v0y we choose the plus sign for the square root, because the vertical component of the initial velocity points upward in Figure 3.13, which is the positive direction. The initial speed v0 and angle q of the baseball are
|
 |
 |
 Interactive LearningWare 3.2 Interactive LearningWare 3.2 | In 1971 astronaut Alan Shepard walked on the moon’s surface. In a moment of whimsy, he hit a golf ball, which was launched upward and followed the familiar trajectory. However, the trajectory differed from what it would have been on earth, because the acceleration due to gravity on the moon is about six times smaller than that on earth. Consider the same ball on earth, launched at the same angle, with the same speed. Find the ratio of (a) the maximum height of the moon-ball to the maximum height of the earth-ball and (b) the range of the moon-ball to the range of the earth-ball. Related Homework: Problems 19, 23 |
|
 |
In projectile motion, the magnitude of the acceleration due to gravity affects the trajectory in a significant way. For example, a baseball or a golf ball would travel much farther and higher on the moon than on the earth, when launched with the same initial velocity. The reason is that the moon’s gravity is only about one-sixth as strong as the earth’s.
Section 2.6 points out that certain types of symmetry with respect to time and speed are present for freely falling bodies. These symmetries are also found in projectile motion, since projectiles are falling freely in the vertical direction. In particular, the time required for a projectile to reach its maximum height H is equal to the time spent returning to the ground. In addition, Figure 3.14 shows that the speed v of the object at any height above the ground on the upward part of the trajectory is equal to the speed v at the same height on the downward part. Although the two speeds are the same, the velocities are different, because they point in different directions. Conceptual Example 9 shows how to use this type of symmetry in your reasoning.
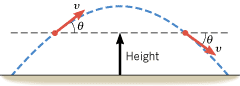 | | Figure 3.14
The speed v of a projectile at a given height above the ground is the same on the upward and downward parts of the trajectory. The velocities are different, however, since they point in different directions. |
|
| Conceptual Example 9 Two Ways to Throw a Stone |
 |
|
From the top of a cliff overlooking a lake, a person throws two stones. The stones have identical initial speeds v0, but stone 1 is thrown downward at an angle q below the horizontal, while stone 2 is thrown upward at the same angle above the horizontal, as Figure 3.15 shows. Neglect air resistance and decide which stone, if either, strikes the water with the greater velocity.
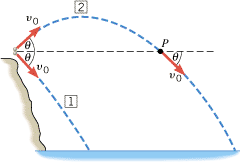 | | Figure 3.15
Two stones are thrown off the cliff with identical initial speeds v0, but at equal angles q that are below and above the horizontal. Conceptual Example 9 compares the velocities with which the stones hit the water below. |
|
Reasoning and Solution We might guess that stone 1, being hurled downward, would strike the water with the greater velocity. To show that this is not true, let’s follow the path of stone 2 as it rises to its maximum height and falls back to earth. Notice point P in the drawing, where stone 2 returns to its initial height; here the speed of stone 2 is v0, but its velocity is directed at an angle q below the horizontal. This is exactly the type of projectile symmetry illustrated in Figure 3.14. At this point, then, stone 2 has a velocity that is identical to the velocity with which stone 1 is thrown downward from the top of the cliff. From this point on, the velocity of stone 2 changes in exactly the same way as that for stone 1, so both stones strike the water with the same velocity.
Related Homework:
Problems 37, 65
|
 |
In all the examples in this section, the projectiles follow a curved trajectory. In general, if the only acceleration is that due to gravity, the shape of the path can be shown to be a parabola.
 |
|
Test your understanding of the material in Sections 3.1, 3.2 and 3.3:
·Motion in Two Dimensions for Constant Acceleration · The Equations of Kinematics ·Projectile Motion
Use Self-Assessment Test 3.1 to check your understanding of these concepts.
|
|
 |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
![]() CONCEPTS AT A GLANCE Following the approach outlined in Figure 3.6, we consider the horizontal and vertical parts of the motion separately. In the horizontal or x direction, the moving object (the projectile) does not slow down in the absence of air resistance. Thus, the x component of the velocity remains constant at its initial value or vx
CONCEPTS AT A GLANCE Following the approach outlined in Figure 3.6, we consider the horizontal and vertical parts of the motion separately. In the horizontal or x direction, the moving object (the projectile) does not slow down in the absence of air resistance. Thus, the x component of the velocity remains constant at its initial value or vx![]() =
=![]() v0x, and the x component of the acceleration is ax
v0x, and the x component of the acceleration is ax![]() =
=![]() 0 m/s2. In the vertical or y direction, however, the projectile experiences the effect of gravity. As a result, the y component of the velocity vy is not constant, but changes. The y component of the acceleration ay is the downward acceleration due to gravity. If the path or trajectory of the projectile is near the earth’s surface, ay has a magnitude of 9.80 m/s2. In this text, then, the phrase “projectile motion” means that ax
0 m/s2. In the vertical or y direction, however, the projectile experiences the effect of gravity. As a result, the y component of the velocity vy is not constant, but changes. The y component of the acceleration ay is the downward acceleration due to gravity. If the path or trajectory of the projectile is near the earth’s surface, ay has a magnitude of 9.80 m/s2. In this text, then, the phrase “projectile motion” means that ax![]() =
=![]() 0 m/s2 and ay equals the acceleration due to gravity, as the Concept-at-a-Glance chart in Figure 3.8 summarizes. Example 2 and other examples in this section illustrate how the equations of kinematics are applied to projectile motion.
0 m/s2 and ay equals the acceleration due to gravity, as the Concept-at-a-Glance chart in Figure 3.8 summarizes. Example 2 and other examples in this section illustrate how the equations of kinematics are applied to projectile motion.![]() =
=![]() +115 m/s throughout the entire descent. Since the plane also travels at a constant horizontal velocity of +115 m/s, it remains directly above the falling package. The pilot always sees the package directly beneath the plane, as the dashed vertical lines in Figure 3.9 show. This result is a direct consequence of the fact that the package has no acceleration in the horizontal direction. In reality, air resistance would slow down the package, and it would not remain directly beneath the plane during the descent. Figure 3.10 further clarifies this point by illustrating what happens to two packages that are released simultaneously from the same height. Package B is given an initial velocity component of v0x
+115 m/s throughout the entire descent. Since the plane also travels at a constant horizontal velocity of +115 m/s, it remains directly above the falling package. The pilot always sees the package directly beneath the plane, as the dashed vertical lines in Figure 3.9 show. This result is a direct consequence of the fact that the package has no acceleration in the horizontal direction. In reality, air resistance would slow down the package, and it would not remain directly beneath the plane during the descent. Figure 3.10 further clarifies this point by illustrating what happens to two packages that are released simultaneously from the same height. Package B is given an initial velocity component of v0x![]() =
=![]() +115 m/s in the horizontal direction, as in Example 2, and the package follows the path shown in the figure. Package A, on the other hand, is dropped from a stationary balloon and falls straight down toward the ground, since v0x
+115 m/s in the horizontal direction, as in Example 2, and the package follows the path shown in the figure. Package A, on the other hand, is dropped from a stationary balloon and falls straight down toward the ground, since v0x![]() =
=![]() 0 m/s. Both packages hit the ground at the same time.
0 m/s. Both packages hit the ground at the same time.
 Concept Simulation 3.1
Concept Simulation 3.1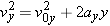 ) to find the maximum height:
) to find the maximum height:
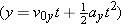
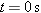 . The solution we seek is
. The solution we seek is 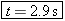 , because
, because 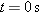 corresponds to the initial kickoff.
corresponds to the initial kickoff.
 Concept Simulation 3.2
Concept Simulation 3.2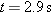 . Since there is no acceleration in the x direction, vx remains constant, and the range is simply the product of
. Since there is no acceleration in the x direction, vx remains constant, and the range is simply the product of 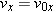 and the time.
and the time.
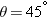 .
.