4.12�Nonequilibrium Applications of Newton's Laws of Motion
When an object is accelerating, it is not in equilibrium. The forces acting on it are not balanced, so the net force is not zero in Newton's second law. However, with one exception, the reasoning strategy followed in solving nonequilibrium problems is identical to that used in equilibrium situations. The exception occurs in Step 4 of the five steps outlined at the beginning of the previous section. Since the object is now accelerating, the representation of Newton's second law in Equations 4.2a and 4.2b applies instead of Equations 4.9a and 4.9b:

and

Example 14 uses these equations in a situation where the forces are applied in directions similar to those in Example 11, except that now an acceleration is present.
EXAMPLE�14Towing a Supertanker
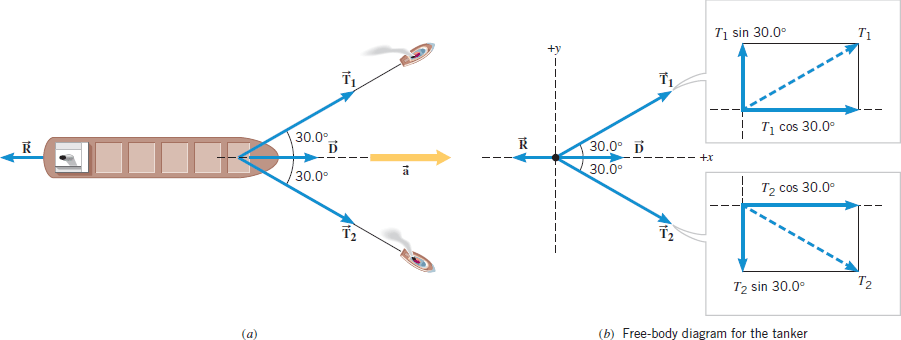
A supertanker of mass  is being towed by two tugboats, as in Figure 4.30a. The tensions in the towing cables apply the forces
is being towed by two tugboats, as in Figure 4.30a. The tensions in the towing cables apply the forces 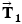 and
and 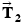 at equal angles of
at equal angles of 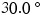 with respect to the tanker's axis. In addition, the tanker's engines produce a forward drive force
with respect to the tanker's axis. In addition, the tanker's engines produce a forward drive force 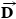 , whose magnitude is
, whose magnitude is 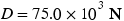 . Moreover, the water applies an opposing force
. Moreover, the water applies an opposing force 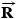 , whose magnitude is
, whose magnitude is 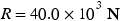 . The tanker moves forward with an acceleration that points along the tanker's axis and has a magnitude of
. The tanker moves forward with an acceleration that points along the tanker's axis and has a magnitude of 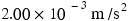 . Find the magnitudes of the tensions
. Find the magnitudes of the tensions 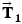 and
and 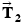 .
.
 and
and  are the tension forces due to the towing cables,
are the tension forces due to the towing cables,  is the forward drive force produced by the tanker's engines, and
is the forward drive force produced by the tanker's engines, and  is the force with which the water opposes the tanker's motion. (b) The free-body diagram for the tanker.
is the force with which the water opposes the tanker's motion. (b) The free-body diagram for the tanker.The unknown forces  and
and 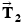 contribute to the net force that accelerates the tanker. To determine
contribute to the net force that accelerates the tanker. To determine 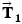 and
and  , therefore, we analyze the net force, which we will do using components. The various force components can be found by referring to the free-body diagram for the tanker in Figure 4.30b, where the ship's axis is chosen as the
, therefore, we analyze the net force, which we will do using components. The various force components can be found by referring to the free-body diagram for the tanker in Figure 4.30b, where the ship's axis is chosen as the 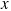 axis. We will then use Newton's second law in its component form,
axis. We will then use Newton's second law in its component form, 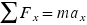 and
and 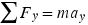 , to obtain the magnitudes of
, to obtain the magnitudes of 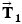 and
and 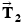 .
.
The individual force components are summarized as follows:
| Force | x Component | y Component |
|---|---|---|
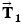 | +T1 cos 30.0� | +T1 sin 30.0� |
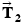 | +T2 cos 30.0� | −T2 sin 30.0� |
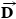 | +D | 0 |
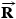 | −R | 0 |
MATH SKILLS�
The sine and cosine functions are defined in Equations 1.1 and 1.2 as 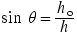 and
and 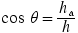 , where
, where 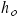 is the length of the side of a right triangle that is opposite the angle
is the length of the side of a right triangle that is opposite the angle 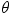 ,
, 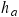 is the length of the side adjacent to the angle
is the length of the side adjacent to the angle 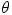 , and
, and 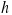 is the length of the hypotenuse (see Figure 4.31a). When using the sine and cosine functions to determine the scalar components of a vector, we begin by identifying the angle
is the length of the hypotenuse (see Figure 4.31a). When using the sine and cosine functions to determine the scalar components of a vector, we begin by identifying the angle 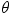 . Figure 4.31b indicates that
. Figure 4.31b indicates that 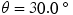 for the vector
for the vector 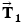 . The components of
. The components of  are
are 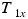 and
and 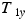 . Comparing the shaded triangles in Figure 4.31, we can see that
. Comparing the shaded triangles in Figure 4.31, we can see that 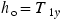 ,
,  , and
, and 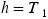 . Therefore, we have
. Therefore, we have


Since the acceleration points along the 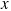 axis, there is no
axis, there is no 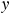 component of the acceleration
component of the acceleration 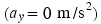 . Consequently, the sum of the
. Consequently, the sum of the 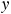 components of the forces must be zero:
components of the forces must be zero:

This result shows that the magnitudes of the tensions in the cables are equal, 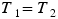 . Since the ship accelerates along the
. Since the ship accelerates along the 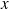 direction, the sum of the
direction, the sum of the 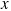 components of the forces is not zero. The second law indicates that
components of the forces is not zero. The second law indicates that

Since 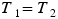 , we can replace the two separate tension symbols by a single symbol
, we can replace the two separate tension symbols by a single symbol 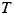 , the magnitude of the tension. Solving for
, the magnitude of the tension. Solving for 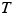 gives
gives
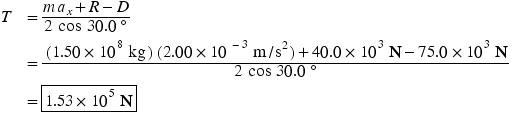
It often happens that two objects are connected somehow, perhaps by a drawbar like that used when a truck pulls a trailer. If the tension in the connecting device is of no interest, the objects can be treated as a single composite object when applying Newton's second law. However, if it is necessary to find the tension, as in the next example, then the second law must be applied separately to at least one of the objects.
EXAMPLE�15Hauling a Trailer
A truck is hauling a trailer along a level road, as Figure 4.32a illustrates. The mass of the truck is 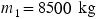 and that of the trailer is
and that of the trailer is 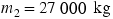 . The two move along the
. The two move along the 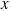 axis with an acceleration of
axis with an acceleration of 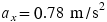 . Ignoring the retarding forces of friction and air resistance, determine
. Ignoring the retarding forces of friction and air resistance, determine
- (a)the tension
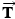 in the horizontal drawbar between the trailer and the truck and
in the horizontal drawbar between the trailer and the truck and - (b)the force
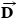 that propels the truck forward.
that propels the truck forward.
 acts on the truck and propels it forward. The drawbar exerts the tension force
acts on the truck and propels it forward. The drawbar exerts the tension force  on the truck and the tension force
on the truck and the tension force  on the trailer. (b) The free-body diagrams for the trailer and the truck, ignoring the vertical forces.
on the trailer. (b) The free-body diagrams for the trailer and the truck, ignoring the vertical forces.Since the truck and the trailer accelerate along the horizontal direction and friction is being ignored, only forces that have components in the horizontal direction are of interest. Therefore, Figure 4.32 omits the weight and the normal force, which act vertically. To determine the tension force  in the drawbar, we draw the free-body diagram for the trailer and apply Newton's second law,
in the drawbar, we draw the free-body diagram for the trailer and apply Newton's second law,  . Similarly, we can determine the propulsion force
. Similarly, we can determine the propulsion force  by drawing the free-body diagram for the truck and applying Newton's second law.
by drawing the free-body diagram for the truck and applying Newton's second law.
Problem-Solving Insight�
A free-body diagram is very helpful when applying Newton's second law. Always start a problem by drawing the free-body diagram.
- (a)The free-body diagram for the trailer is shown in Figure 4.32b. There is only one horizontal force acting on the trailer, the tension force
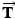 due to the drawbar. Therefore, it is straightforward to obtain the tension from
due to the drawbar. Therefore, it is straightforward to obtain the tension from 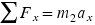 , since the mass of the trailer and the acceleration are known:
, since the mass of the trailer and the acceleration are known:
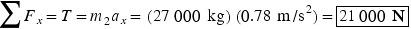
- (b)Two horizontal forces act on the truck, as the free-body diagram in Figure 4.32b shows. One is the desired force
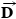 . The other is the force
. The other is the force 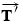 . According to Newton's third law,
. According to Newton's third law, 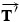 is the force with which the trailer pulls back on the truck, in reaction to the truck pulling forward. If the drawbar has negligible mass, the magnitude of
is the force with which the trailer pulls back on the truck, in reaction to the truck pulling forward. If the drawbar has negligible mass, the magnitude of 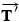 is equal to the magnitude of
is equal to the magnitude of 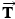 —namely, 21 000 N. Since the magnitude of
—namely, 21 000 N. Since the magnitude of 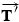 , the mass of the truck, and the acceleration are known,
, the mass of the truck, and the acceleration are known,  can be used to determine the drive force:
can be used to determine the drive force:

In Section 4.11 we examined situations where the net force acting on an object is zero, and in the present section we have considered two examples where the net force is not zero. Conceptual Example 16 illustrates a common situation where the net force is zero at certain times but is not zero at other times.
CONCEPTUAL EXAMPLE�16The Motion of a Water Skier
Figure 4.33 shows a water skier at four different moments:
- (a)The skier is floating motionless in the water.
- (b)The skier is being pulled out of the water and up onto the skis.
- (c)The skier is moving at a constant speed along a straight line.
- (d)The skier has let go of the tow rope and is slowing down.

For each moment, explain whether the net force acting on the skier is zero.
- (a)The skier is floating motionless in the water, so her velocity and acceleration are both zero. Therefore, the net force acting on her is zero, and she is in equilibrium.
- (b)As the skier is being pulled up and out of the water, her velocity is increasing. Thus, she is accelerating, and the net force acting on her is not zero. The skier is not in equilibrium. The direction of the net force is shown in Figure 4.33b.
- (c)The skier is now moving at a constant speed along a straight line (Figure 4.33c), so her velocity is constant. Since her velocity is constant, her acceleration is zero. Thus, the net force acting on her is zero, and she is again in equilibrium, even though she is moving.
- (d)After the skier lets go of the tow rope, her speed decreases, so she is decelerating. Thus, the net force acting on her is not zero, and she is not in equilibrium. The direction of the net force is shown in Figure 4.33d.
Related Homework: Problem 75
The force of gravity is often present among the forces that affect the acceleration of an object. Examples 17 and 18 deal with typical situations.
EXAMPLE�17Accelerating Blocks
Block 1 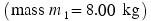 is moving on a frictionless
is moving on a frictionless 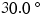 incline. This block is connected to block 2
incline. This block is connected to block 2 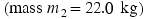 by a massless cord that passes over a massless and frictionless pulley (see Figure 4.34a). Find the acceleration of each block and the tension in the cord.
by a massless cord that passes over a massless and frictionless pulley (see Figure 4.34a). Find the acceleration of each block and the tension in the cord.

 , the normal force
, the normal force  , and the force
, and the force  due to the tension in the cord. Two forces act on block 2: its weight
due to the tension in the cord. Two forces act on block 2: its weight  and the force
and the force  due to the tension. The acceleration is labeled according to its magnitude
due to the tension. The acceleration is labeled according to its magnitude  . (b) Free-body diagrams for the two blocks.
. (b) Free-body diagrams for the two blocks.Since both blocks accelerate, there must be a net force acting on each one. The key to this problem is to realize that Newton's second law can be used separately for each block to relate the net force and the acceleration. Note also that both blocks have accelerations of the same magnitude  , since they move as a unit. We assume that block 1 accelerates up the incline and choose this direction to be the
, since they move as a unit. We assume that block 1 accelerates up the incline and choose this direction to be the  axis. If block 1 in reality accelerates down the incline, then the value obtained for the acceleration will be a negative number.
axis. If block 1 in reality accelerates down the incline, then the value obtained for the acceleration will be a negative number.
Problem-Solving Insight�
Mass and weight are different quantities. They cannot be interchanged when solving problems.
Three forces act on block 1: (1) 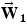 is its weight
is its weight  , (2)
, (2) 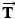 is the force applied because of the tension in the cord, and (3)
is the force applied because of the tension in the cord, and (3) 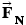 is the normal force the incline exerts. Figure 4.34b shows the free-body diagram for block 1. The weight is the only force that does not point along the
is the normal force the incline exerts. Figure 4.34b shows the free-body diagram for block 1. The weight is the only force that does not point along the 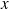 ,
, 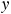 axes, and its
axes, and its  and
and 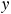 components are given in the diagram. Applying Newton's second law
components are given in the diagram. Applying Newton's second law 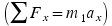 to block 1 shows that
to block 1 shows that

where we have set 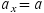 . This equation cannot be solved as it stands, since both
. This equation cannot be solved as it stands, since both 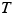 and
and 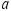 are unknown quantities. To complete the solution, we next consider block 2.
are unknown quantities. To complete the solution, we next consider block 2.
Two forces act on block 2, as the free-body diagram in Figure 4.34b indicates: (1) 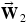 is its weight
is its weight  and (2)
and (2) 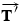 is exerted as a result of block 1 pulling back on the connecting cord. Since the cord and the frictionless pulley are massless, the magnitudes of
is exerted as a result of block 1 pulling back on the connecting cord. Since the cord and the frictionless pulley are massless, the magnitudes of 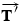 and
and 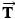 are the same:
are the same:  . Applying Newton's second law
. Applying Newton's second law  to block 2 reveals that
to block 2 reveals that

The acceleration 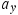 has been set equal to
has been set equal to 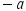 since block 2 moves downward along the
since block 2 moves downward along the 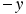 axis in the free-body diagram, consistent with the assumption that block 1 moves up the incline. Now there are two equations in two unknowns, and they may be solved simultaneously (see Appendix C) to give
axis in the free-body diagram, consistent with the assumption that block 1 moves up the incline. Now there are two equations in two unknowns, and they may be solved simultaneously (see Appendix C) to give 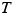 and
and 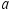 :
:

MATH SKILLS�
The two equations containing the unknown quantities  and
and 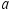 are
are

Neither equation by itself can yield numerical values for 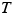 and
and 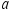 . However, the two equations can be solved simultaneously in the following manner. To begin with, we rearrange Equation (1) to give
. However, the two equations can be solved simultaneously in the following manner. To begin with, we rearrange Equation (1) to give 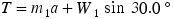 . Next, we substitute this result into Equation (2) and obtain a result containing only the unknown acceleration
. Next, we substitute this result into Equation (2) and obtain a result containing only the unknown acceleration  :
:

Rearranging this equation so that the terms 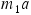 and
and 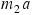 stand alone on the left of the equals sign, we have
stand alone on the left of the equals sign, we have

This result yields the value of 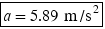 . We can also substitute the expression for
. We can also substitute the expression for 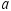 into either one of the two starting equations and obtain a result containing only the unknown tension
into either one of the two starting equations and obtain a result containing only the unknown tension 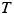 . We choose Equation (1) and find that
. We choose Equation (1) and find that

Solving for 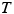 gives
gives
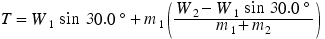
This expression yields the value of 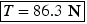 .
.
EXAMPLE�18Hoisting a Scaffold
A window washer on a scaffold is hoisting the scaffold up the side of a building by pulling downward on a rope, as in Figure 4.35a. The magnitude of the pulling force is 540 N, and the combined mass of the worker and the scaffold is 155 kg. Find the upward acceleration of the unit.

 results from the effort of the window washer and acts on him and the scaffold in three places, as discussed in Example 18. (b) The free-body diagram of the unit comprising the man and the scaffold.
results from the effort of the window washer and acts on him and the scaffold in three places, as discussed in Example 18. (b) The free-body diagram of the unit comprising the man and the scaffold.The worker and the scaffold form a single unit, on which the rope exerts a force in three places. The left end of the rope exerts an upward force 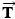 on the worker's hands. This force arises because he pulls downward with a 540-N force, and the rope exerts an oppositely directed force of equal magnitude on him, in accord with Newton's third law. Thus, the magnitude
on the worker's hands. This force arises because he pulls downward with a 540-N force, and the rope exerts an oppositely directed force of equal magnitude on him, in accord with Newton's third law. Thus, the magnitude 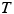 of the upward force is
of the upward force is 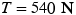 and is the magnitude of the tension in the rope. If the masses of the rope and each pulley are negligible and if the pulleys are friction-free, the tension is transmitted undiminished along the rope. Then, a 540-N tension force
and is the magnitude of the tension in the rope. If the masses of the rope and each pulley are negligible and if the pulleys are friction-free, the tension is transmitted undiminished along the rope. Then, a 540-N tension force 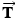 acts upward on the left side of the scaffold pulley (see part a of the drawing). A tension force is also applied to the point
acts upward on the left side of the scaffold pulley (see part a of the drawing). A tension force is also applied to the point 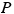 , where the rope attaches to the roof. The roof pulls back on the rope in accord with the third law, and this pull leads to the 540-N tension force
, where the rope attaches to the roof. The roof pulls back on the rope in accord with the third law, and this pull leads to the 540-N tension force 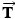 that acts on the right side of the scaffold pulley. In addition to the three upward forces, the weight of the unit must be taken into account
that acts on the right side of the scaffold pulley. In addition to the three upward forces, the weight of the unit must be taken into account 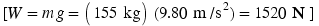 . Part b of the drawing shows the free-body diagram.
. Part b of the drawing shows the free-body diagram.
Newton's second law 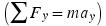 can be applied to calculate the acceleration
can be applied to calculate the acceleration 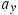 :
:

Check Your Understanding�
A circus performer hangs stationary from a rope. She then begins to climb upward by pulling herself up, hand over hand. When she starts climbing, is the tension in the rope
- (a)less than,
- (b)equal to, or
- (c)greater than it is when she hangs stationary?
A freight train is accelerating on a level track. Other things being equal, would the tension in the coupling between the engine and the first car change if some of the cargo in the last car were transferred to any one of the other cars?
Two boxes have masses 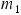 and
and 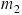 , and
, and 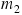 is greater than
is greater than 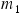 . The boxes are being pushed across a frictionless horizontal surface. As the drawing shows, there are two possible arrangements, and the pushing force is the same in each. In which arrangement,
. The boxes are being pushed across a frictionless horizontal surface. As the drawing shows, there are two possible arrangements, and the pushing force is the same in each. In which arrangement,
- (a)or
- (b), does the force that the left box applies to the right box have a greater magnitude, or
- (c)is the magnitude the same in both cases?

