4.5�Newton's Third Law of Motion
Imagine you are in a football game. You line up facing your opponent, the ball is snapped, and the two of you crash together. No doubt, you feel a force. But think about your opponent. He too feels something, for while he is applying a force to you, you are applying a force to him. In other words, there isn't just one force on the line of scrimmage; there is a pair of forces. Newton was the first to realize that all forces occur in pairs and there is no such thing as an isolated force, existing all by itself. His third law of motion deals with this fundamental characteristic of forces.
Newton's Third Law of Motion
Whenever one object exerts a force on a second object, the second object exerts an oppositely directed force of equal magnitude on the first object.
Figure 4.7 illustrates how the third law applies to an astronaut who is drifting just outside a spacecraft and who pushes on the spacecraft with a force  . According to the third law, the spacecraft pushes back on the astronaut with a force
. According to the third law, the spacecraft pushes back on the astronaut with a force  that is equal in magnitude but opposite in direction. In Example 4, we examine the accelerations produced by each of these forces.
that is equal in magnitude but opposite in direction. In Example 4, we examine the accelerations produced by each of these forces.
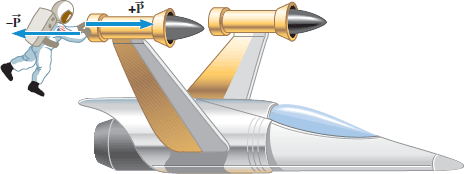
 . According to Newton's third law, the spacecraft simultaneously pushes back on the astronaut with a force
. According to Newton's third law, the spacecraft simultaneously pushes back on the astronaut with a force 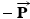 .
.EXAMPLE�4The Accelerations Produced by Action and Reaction Forces
Suppose that the mass of the spacecraft in Figure 4.7 is  and that the mass of the astronaut is
and that the mass of the astronaut is  . In addition, assume that the astronaut pushes with a force of
. In addition, assume that the astronaut pushes with a force of  on the spacecraft. Find the accelerations of the spacecraft and the astronaut.
on the spacecraft. Find the accelerations of the spacecraft and the astronaut.
Consistent with Newton's third law, when the astronaut applies the force  to the spacecraft, the spacecraft applies a reaction force
to the spacecraft, the spacecraft applies a reaction force  to the astronaut. As a result, the spacecraft and the astronaut accelerate in opposite directions. Although the action and reaction forces have the same magnitude, they do not create accelerations of the same magnitude, because the spacecraft and the astronaut have different masses. According to Newton's second law, the astronaut, having a much smaller mass, will experience a much larger acceleration. In applying the second law, we note that the net force acting on the spacecraft is
to the astronaut. As a result, the spacecraft and the astronaut accelerate in opposite directions. Although the action and reaction forces have the same magnitude, they do not create accelerations of the same magnitude, because the spacecraft and the astronaut have different masses. According to Newton's second law, the astronaut, having a much smaller mass, will experience a much larger acceleration. In applying the second law, we note that the net force acting on the spacecraft is  , while the net force acting on the astronaut is
, while the net force acting on the astronaut is  .
.
Using the second law, we find that the acceleration of the spacecraft is
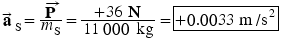
The acceleration of the astronaut is
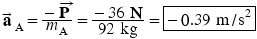
Problem-Solving Insight�
Even though the magnitudes of the action and reaction forces are always equal, these forces do not necessarily produce accelerations that have equal magnitudes, since each force acts on a different object that may have a different mass.
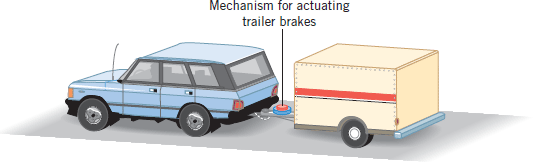
The physics of automatic trailer brakes. There is a clever application of Newton's third law in some rental trailers. As Figure 4.8 illustrates, the tow bar connecting the trailer to the rear bumper of a car contains a mechanism that can automatically actuate brakes on the trailer wheels. This mechanism works without the need for electrical connections between the car and the trailer. When the driver applies the car brakes, the car slows down. Because of inertia, however, the trailer continues to roll forward and begins pushing against the bumper. In reaction, the bumper pushes back on the tow bar. The reaction force is used by the mechanism in the tow bar to “push a brake pedal” for the trailer.
Check Your Understanding�
A father and his seven-year-old daughter are facing each other on ice skates. With their hands, they push off against one another. Which one or more of the following statements is (are) true?
- (a)Each experiences an acceleration that has a different magnitude.
- (b)Each experiences an acceleration of the same magnitude.
- (c)Each experiences a pushing force that has a different magnitude.
- (d)Each experiences a pushing force that has the same magnitude.
