4.3 Newton's Second Law of Motion
Newton's first law indicates that if no net force acts on an object, then the velocity of the object remains unchanged. The second law deals with what happens when a net force does act. Consider a hockey puck once again. When a player strikes a stationary puck, he causes the velocity of the puck to change. In other words, he makes the puck accelerate. The cause of the acceleration is the force that the hockey stick applies. As long as this force acts, the velocity increases, and the puck accelerates. Now, suppose another player strikes the puck and applies twice as much force as the first player does. The greater force produces a greater acceleration. In fact, if the friction between the puck and the ice is negligible, and if there is no wind resistance, the acceleration of the puck is directly proportional to the force. Twice the force produces twice the acceleration. Moreover, the acceleration is a vector quantity, just as the force is, and points in the same direction as the force.
Often, several forces act on an object simultaneously. Friction and wind resistance, for instance, do have some effect on a hockey puck. In such cases, it is the net force, or the vector sum of all the forces acting, that is important. Mathematically, the net force is written as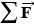 
, where the Greek capital letter 
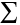(sigma) denotes the vector sum. Newton's second law states that the acceleration is proportional to the net force acting on the object.
In Newton's second law, the net force is only one of two factors that determine the acceleration. The other is the inertia or mass of the object. After all, the same net force that imparts an appreciable acceleration to a hockey puck (small mass) will impart very little acceleration to a semitrailer truck (large mass). Newton's second law states that for a given net force, the magnitude of the acceleration is inversely proportional to the mass. Twice the mass means one-half the acceleration, if the same net force acts on both objects. Thus, the second law shows how the acceleration depends on both the net force and the mass, as given in Equation 4.1.
Newton's Second Law of Motion
When a net external force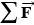 
acts on an object of mass 
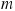, the acceleration 
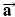that results is directly proportional to the net force and has a magnitude that is inversely proportional to the mass. The direction of the acceleration is the same as the direction of the net force.
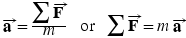
SI Unit of Force: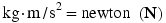 
Note that the net force in Equation 4.1 includes only the forces that the environment exerts on the object of interest. Such forces are called external forces. In contrast, internal forces are forces that one part of an object exerts on another part of the object and are not included in Equation 4.1.
According to Equation 4.1, the SI unit for force is the unit for mass (kg) times the unit for acceleration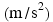 
, or
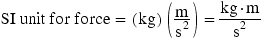
The combination of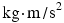 
is called a newton (N) and is a derived SI unit, not a base unit; 
.
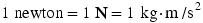In the CGS system, the procedure for establishing the unit of force is the same as with SI units, except that mass is expressed in grams (g) and acceleration in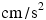 
. The resulting unit for force is the dyne; 
.
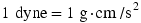 | Concept Simulation 4.1: Newton's Second Law |
In the BE system, the unit for force is defined to be the pound (lb),1 and the unit for acceleration is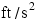 
. With this procedure, Newton's second law can then be used to obtain the BE unit for mass:
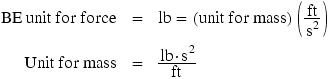
The combination of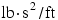 
is the unit for mass in the BE system and is called the slug (sl); 
.
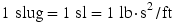Table 4.1 summarizes the various units for mass, acceleration, and force. Conversion factors between force units from different systems are provided on the page facing the inside of the front cover.
| System | Mass | Acceleration | Force |
|---|---|---|---|
| SI | kilogram (kg) | meter/second2 (m/s2) | newton (N) |
| CGS | gram (g) | centimeter/second2 (cm/s2) | dyne (dyn) |
| BE | slug (sl) | foot/second2 (ft/s2) | pound (lb) |
When using the second law to calculate the acceleration, it is necessary to determine the net force that acts on the object. In this determination a free-body diagram helps enormously. A free-body diagram is a diagram that represents the object and the forces that act on it. Only the forces that act on the object appear in a free-body diagram. Forces that the object exerts on its environment are not included. Example 1 illustrates the use of a free-body diagram.
EXAMPLE 1Pushing a Stalled Car
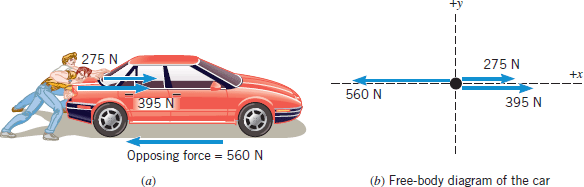
Two people are pushing a stalled car, as Figure 4.5a indicates. The mass of the car is 1850 kg. One person applies a force of 275 N to the car, while the other applies a force of 395 N. Both forces act in the same direction. A third force of 560 N also acts on the car, but in a direction opposite to that in which the people are pushing. This force arises because of friction and the extent to which the pavement opposes the motion of the tires. Find the acceleration of the car.
 | Animated Figure 4.5 |
According to Newton's second law, the acceleration is the net force divided by the mass of the car. To determine the net force, we use the free-body diagram in Figure 4.5b. In this diagram, the car is represented as a dot, and its motion is along the 
axis. The diagram makes it clear that the forces all act along one direction. Therefore, they can be added as colinear vectors to obtain the net force.
From Equation 4.1, the acceleration is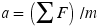 
. The net force is
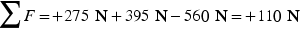
The acceleration can now be obtained:
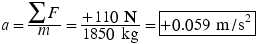
The plus sign indicates that the acceleration points along the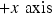 
, in the same direction as the net force.
Problem-Solving Insight
The direction of the acceleration is always the same as the direction of the net force.
Check Your Understanding
The net external force acting on an object is zero. Which one of the following statements is true?
- (a)The object can only be stationary.
- (b)The object can only be traveling with a constant velocity.
- (c)The object can be either stationary or traveling with a constant velocity.
- (d)The object can only be traveling with a velocity that is changing.
In Case A an object is moving straight downward with a constant speed of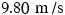 
, while in Case B an object is moving straight downward with a constant acceleration of magnitude 
. Which one of the following is true?
- (a)A nonzero net external force acts on the object in both cases.
- (b)A nonzero net external force acts on the object in neither case.
- (c)A nonzero net external force acts on the object in Case A only.
- (d)A nonzero net external force acts on the object in Case B only.