Archimedes' Principle

Objective

•
to confirm Archimedes' Principle for objects of different densities
(ρ_object > ρ_fluid)
and
(ρ_object < ρ_fluid)
•
to determine the density of unknown materials using Archimedes' Principle

Equipment

force sensor, a beaker, a graduated cylinder, electronic balance, string, masking tape, overflow can, catch can, different objects (wood cube, rubber stopper, golf ball), water, rods and base, GA software

Figure 1

Figure 2

Introduction and Theory

When an object is immersed in a fluid, it feels lighter than when it is in the air. The surrounding fluid presses against the object from all directions. The sideways forces would be balanced and oppose each other equally. The upward and downward forces would not be the same because the fluid pressure increases with the depth. In fluid, the pressure at the bottom of the object will be greater than the pressure at the top of the object due to the weight of the layers of fluid between the top and bottom parts of the object.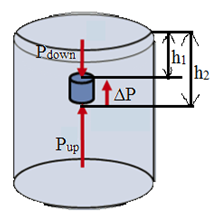

Figure 3

The gauge pressure (ΔP) is given by the following equations.

( 1 )

ΔP = P_down − P_up

( 2 )

ΔP = ρ_f g(h₂ − h₁)

The gauge pressure is a function of depth h. The unit of pressure is the Pascal (Pa). As a result of the pressure difference, there is an upward buoyant force F_b that acts on the fully or partially submerged object (Fig. 4).

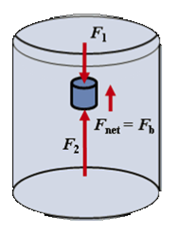
Figure 4

In the special case of an object such as a cylinder oriented flat side down, the buoyant force equals the product of the gauge pressure and the top surface area.

( 3 )

F_b = ΔPA

( 4 )

F_b = ρ_f g(h₂ − h₁)A

Considering that

(h₂ − h₁) = h

is the height of the submerged cylinder, we get hA = V_o. Hence, the buoyant force can be found using the equation

( 5 )

F_b = ρ_f gV_o,

where ρ_f is the density of fluid (kg/m³) and V_o is the volume of the submerged part of the object (m³). The buoyant force depends on the density of the liquid and the volume of the object submerged in the fluid, but not its weight or shape. If the density of the object is greater than that of the fluid, the object will sink. If the density of the object is equal to that of the fluid, the object will neither sink nor float. If the density of the object is less than that of the fluid, the object will float. When the object is placed in the fluid, the fluid gets displaced. The displaced fluid has weight

( 6 )

W_f = m_f g,

where m_f is the mass of the displaced fluid. The mass m_f of the fluid can be expressed in terms of its density ρ_f and volume V_f.

( 7 )

m_f = ρ_f V_f

Hence,

( 8 )

W_f = ρ_f gV_f = F_b.

Equation 8 expresses Archimedes' Principle.

Archimedes' Principle: Any object, wholly or partly immersed in a fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object.

From this principle, we can see that whether an object floats or sinks in water is not based on its own weight, but the amount of water it displaces. That is why a very heavy ocean liner can float. It displaces a large amount of water. The weight of the object submerged in the fluid is called apparent weight

W_app,

and it is equal to the difference between the weight of the object in the air W_o and the buoyant force F_b.

( 9 )

W_app = W_o − F_b

Video

View the video below prior to beginning your lab.

Procedure

Please print the worksheet for this lab. Answer all the questions on the Lab Worksheet prior to submitting the Inlab in WebAssign.

Checkpoint:
Be sure to have your TA sign your lab worksheet, printed Inlab, and all printed graphs after each part is completed. Be sure the data can be seen on the graphs.

Part 1: Archimedes' Principle

Place the force sensor on the horizontal rod that is attached to the vertical stand. In order for the sensor to work properly, it has to be calibrated. Open the DataStudio program: Desktop/pirt inst labs/PHY 113/PreSet Up Labs/Fluid Mechanics.

Force Sensor Calibration Procedure

1
In the DataStudio program, open "Setup," put a check mark next to the "Force sensor" as a sensor connected to channel A. Choose "Calibrate Sensor," then "2-Point Calibration."
2
With nothing hanging from the sensor, set the first value to be zero, then press the Tare button on the force sensor itself, and finally select "Read from Sensor" in DataStudio. The Tare button sets up a zero on the force sensor.
3
To set up a second value, hang a 1.00-kg mass (or other mass provided) from the sensor. Set the second value of calibration point in DataStudio to be equal to the gravitational force applied to the hanging weight. Select "Read from Sensor."
4
Click OK. Close the setup window.
5
Check your calibration by taking 5 seconds of data with the 1.00-kg mass hanging from the sensor. If you see a horizontal line (a line with a zero slope) drawn at the magnitude of the force level, the force sensor is calibrated and ready to take measurements of the force.

Measure the mass of the empty catch can. The catch can will be used to collect water displaced by the submerged object. Record the mass in the Inlab.

Figure 5

Place the overflow can under the force sensor. Place a beaker under the angled overflow spout. Fill the overflow can with room temperature tap water just above the spout until it begins to overflow. Wait for the dripping from the overflow spout to stop. Remove the beaker and place the catch can under the overflow spout instead.

Zero/Tare the force sensor. Use a string to suspend object 1

(ρ_object > ρ_fluid)

from the force sensor. Position the object slightly above the water surface in the overflow can.

Click Start. If there is some fluctuation in the data, wait for the data to become more stable. Leave DataStudio in the recording mode. Slowly move down a rod with a force sensor to fully submerge the object in the water. Wait until the dripping from the overflow stops. Record the mean value of the weight of the object in the air W_o (N) and the mean value of the apparent weight of the object W_app (N) in Table 1 in the Inlab. (Hint: Select the part of the graph where the force seems to be constant, and then choose "Statistics" from the menu bar.)

Measure the mass M of the catch can with the displaced water. Record the mass of the catch can and displaced water in Table 1 in the Inlab. Also measure the volume V of the water in the catch can. Record this value in Table 1 in the Inlab.

Dump the water from the beaker, and then dry the beaker with the paper towel.

Replace the first object with the second provided object

(ρ_object < ρ_fluid).

Repeat steps 3–7. Record all data in Table 1 in the Inlab.

Both sets of experimental data will be used to calculate the weight of the displaced water, equation 6

W_f = m_f g,

, the magnitude of the buoyant force twice, first using equation 5

F_b = ρ_f gV_o,

and then using equation 9

W_app = W_o − F_b

, and then to find the percentage differences between the weight of the displaced water and the magnitude of the buoyant force in each case. Submit all your answers in the Inlab.

Part 2: Determine the density of the golf ball.

Measure the mass of a golf ball with an electronic balance. Record the mass in Table 3 in the Inlab.

Use the same procedure from Part 1 to measure the weight of the object in the air and its apparent weight after submerging the object in the water in the overflow can. Record the mean value of both forces in Table 3 in the Inlab.

Find the magnitude of the buoyant force acting on the golf ball. Then find the density of the golf ball using the density equation and Archimedes' Principle. (Hint: Combine equations 9

W_app = W_o − F_b

and 5

F_b = ρ_f gV_o,

to find the volume of the water displaced by the object. The volume of the displaced water equals the volume of the object.)

The theoretical value of the golf ball's density is 1130 kg/m³. Find the percent discrepancy between the theoretical and experimental values of the golf ball's density. Submit your answer in the Inlab.

Part 3: What is the mass of the system?

Pour 150 mL of water into a beaker.

Place the beaker with water on the electronic balance. Measure their total mass and record it in Table 4 in the Inlab.

Use what you learned about the buoyant force to predict what the reading on the balance will be if you hang a golf ball of known mass so that it's completely immersed in the water without touching the bottom of the beaker. No water should overflow from the beaker.

Go ahead and try it. Does the result match your prediction within the uncertainty?

In the Postlab discussion, explain the meaning of the result shown by the electronic balance. Explain the reason for any major discrepancy between your predicted and experimental results.

Adapted from PASCO scientific at pasco.com.