Linear Motion

Objectives

•
to compare the relationship between position vs. time and velocity vs. time for different types of linear motion
•
to measure the value of gravitational acceleration g on Earth by the free fall method and compare it to the accepted value

Equipment

battery-powered constant speed cart, masking tape, cardboard, PASCO motion sensor, fan cart, track Spring Semester: small rubber object or whiffle ball, stop watch, 30-m measuring tape

Figure 1: Spring Semester Equipment

Fall Semester: picket fence with 5-cm band spacing, wide photogate on stand, floor mat

Figure 2: Fall Semester Equipment

Introduction and Theory

Kinematics is the area of physics that studies types of motion without specifying what caused it. The three major types of simple linear motion are constant velocity motion, uniformly accelerated linear motion, and free fall. The basic physics quantities used to describe the motion of an object are: position, distance, displacement, speed, velocity, and acceleration. The description is sufficient if one can specify the location of the object at any specific time. There are a number of ways of representing motion. One of them is to use a motion diagram. Fig. 3 presents a motion diagram of an object moving at constant acceleration. Each dot presents a position of an object registered in an equal time interval.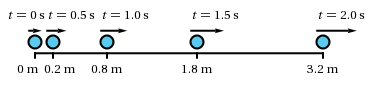

Figure 3: Motion Diagram for Constant Acceleration

The most useful way is graphing position x, velocity v, and acceleration a vs. time t, as the rise and fall of the graph is clearly analogous to the changes in these quantities.

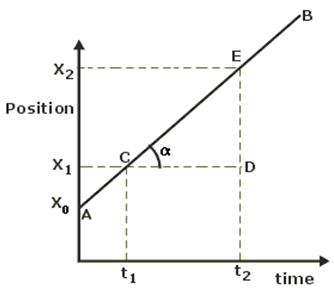
Figure 4: Position vs. Time Plot

If the position vs. time graph is presented as a linear graph, it indicates that the object was moving with a constant velocity. In this case, velocity can be found as a slope of the position vs. time graph.

( 1 )

slope = velocity =

x₂ − x₁

t₂ − t₁

= tan α

The equation used to specify the location of the object at any time is presented as position being a function of time. The equation of motion shows how the position changes with time passed. For constant speed motion, the position is a linear function of time

( 2 )

x(t) = x₀ + vt,

where x₀ is the initial position, and v is the constant velocity of the object's motion. In a wide range of motions, the velocity can change from moment to moment. Fig. 3 is a motion diagram of uniformly accelerated motion or motion with constant acceleration. To provide a measure of how much the velocity changes in time, we introduce the concept of acceleration. The average acceleration is a vector that points in the same direction as the change in the velocity. The SI unit of acceleration is m/s².

( 3 )

average acceleration =

change in velocity

elapsed time

or a_ave =

v₂ − v₁

t₂ − t₁

In case of motion with constant acceleration, velocity is a linear function of time.

( 4 )

v = v₀ + at

In Fig. 5, the slope of the line tangent to the graph represents acceleration at time t.

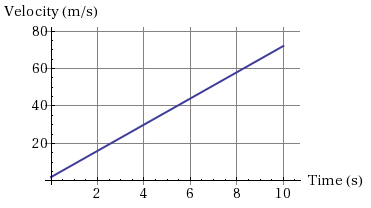
Figure 5: v(t) Graph

The position at any given instant of time t of an object moving with constant acceleration a, having initial position x₀ and initial velocity v₀, can be found as

( 5 )

x = x₀ + v₀t +

at².

In this case, position is a quadratic function of time. Consider the picture in Fig. 6. An object at rest is released from a position of y above the floor.

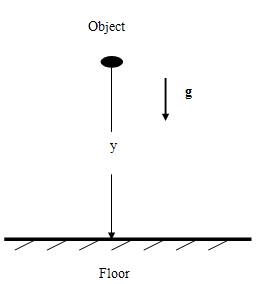
Figure 6

If air resistance is negligible, the motion of the object caused by the gravitational force is known as free fall.

Fig. 7

presents a motion diagram of the free fall motion of the object before it reaches terminal velocity. This diagram has a similar view as the one for the uniformly accelerated motion above. A free-falling object experiences a uniformly accelerated motion until it reaches its terminal velocity.

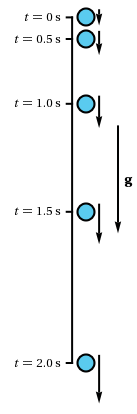
Figure 7: Motion Diagram for Free Fall

Everything on Earth experiences gravitational acceleration from the Earth. The acceleration of a freely falling object, g, is constant and equals approximately 9.81 m/s² near the surface of the Earth. Since free fall motion is uniformly accelerated motion, the equations of kinematics that describe uniformly accelerated motion can also be used. The object falls down to the floor after time t. Eqn. 6 describes the change in the object's position with time

( 6 )

y(t) = y₀ + v₀t +

gt²

where g is the gravitational acceleration. Considering that the dropped object has zero initial velocity and y₀ is zero, the equation can be simplified to

( 7 )

y(t) =

gt²

In this lab, you will measure the magnitude of the gravitational acceleration and write equations that describe motion of different objects.

Video

View the video below prior to beginning your lab.

Procedure

Please print the worksheet for this lab. Answer all the questions on the Lab Worksheet prior to submitting the Inlab in WebAssign.

Checkpoint:
Print only the section of the worksheet that applies to your semester. Be sure to have your TA sign your lab worksheet, printed Inlab, and all printed graphs after each part is completed. Be sure the data can be seen on the graphs.

Part 1: The cart moves toward the motion sensor at a constant speed.

On the lab worksheet, sketch the graphs you expect to be produced by the cart moving toward the motion sensor with constant speed.

Turn on the interface. Open the presetup file "Linear Motion" located at Desktop/pirt inst labs/PHY 113/PreSet Up Labs/Linear Motion. Be sure the Start button shows active in the software. To calibrate the motion sensor: Click Calibrate Sensor, and then click on Motion Sensor. Type "standard distance 1m." Place a 1-m ruler between the sensor and the cart. Remove the ruler and click set the standard distance. You should see 1 m appears in the window on the screen. Close the calibration window.

Place the constant speed cart at the opposite end of the track from the motion sensor. Using masking tape, make a mark on the track 20 cm away from the motion sensor. Turn on and hold the cart. Click Start in the Data Studio software and release the cart. Stop the recording when the cart reaches a 20-cm mark. In a group, discuss what kind of graphs were produced by the motion of the cart. Do they look as you expected them to look? Record the major points of your discussion in the worksheet for this lab.

Figure 8

You should see on the screen the position vs. time graph and velocity vs. time graph of the cart's run produced by the software. Use the "Autofit" function to resize the graphs.

Figure 9

On the position vs. time graph, highlight (drag around with the computer cursor) the part of the plot corresponding to the cart moving along the track with constant speed. Apply "Linear Fit." (Hint: Select "Linear Fit" in the pull-down Fit menu.)

Figure 10

Login to your WebAssign account. Open the Linear Motion Inlab and complete Table 1. Complete all of the following questions for "Part 1: Constant Velocity Motion." Take a screenshot of the graphs with the data from "Linear Fit." Paste and save them in a document in DOC format. Upload this file in the Inlab for Part 1.

Part 2: Uniformly Accelerated Motion

On the lab worksheet, sketch the graphs you expect to be produced by the sail cart moving away from the motion sensor with constant acceleration.

Attach a piece of the cardboard to the side of the fan cart facing the motion sensor. Place the fan cart 20 cm away from the motion sensor and oriented so that it will move away from the motion sensor. Turn on the fan and start the program. Stop recording the data when the cart reaches the other end of the track. Stop the cart. In a group, discuss what kind of graphs are produced by the motion of the cart. Do they look as you expected them to look? Compare these graphs to the ones received in Part 1. Record the major points of your discussion on the worksheet for this lab.

Figure 11

On the position vs. time graph, highlight the curved part of the graph corresponding to the cart accelerating along the track. Fit the selected part of the data with a "Quadratic Fit" function.

Figure 12

Complete Table 2 in the Linear Motion Inlab in WebAssign. Answer all the following questions for this part of the lab. Take a screenshot of the graphs with the data from "Quadratic Fit." Paste and save them in a document in DOC format. Upload this file in the Inlab for Part 2.

Part 3: Free Fall

Caution:
Depending on the semester you take the lab, you will either do the Free Fall Experiment A. Stairway or B. Photogate.

A. Stairway (Spring Semester)

Drop the provided object from the stairway of a building. Make sure that no one is directly below the object when it is dropped. Use a tape measure to determine the height y from which the object is released. Use the stopwatch to measure the time t it takes for the object to fall down to the ground. These measurements have to be repeated at least 6 times in order to get a reasonable value of

along with the associated error.

Figure 13

Record measurements of the height and time on the lab worksheet. Assume the error in height is 2.0 cm.

In GA, enter the values of time. Use "Statistics" to find the mean value of time and standard deviation. Take a screenshot of the statistics graphs with the provided data. Paste and save them in a document in DOC format. Upload this file in the Inlab for Part 3. Using these data, you will evaluate the value of gravitational acceleration g that each object has experienced, and its uncertainty.

Complete Part 3 in the Linear Motion Inlab in WebAssign. Be sure to upload a statistics graph from GA. Discuss with your group members if the experimental value of g agrees with the expected one. Record the major points of your discussion on the lab worksheet.

B. Photogate (Fall Semester)

Turn on the interface and open the pre-set experiment file: Desktop/Labs/PHY 113/PreSetUp Files/Free Fall.

Figure 14

Position the stand with a photogate at the edge of the lab table in such a way that you can safely drop the long picket fence all the way through. Bring the rubber or foam pad directly underneath the photogate onto the floor to cushion the landing of the picket fence. Try to catch the picket fence after it passes through the photogate.

Press the Start button and carefully drop the picket fence through the photogate. (See Appendix B for more information.) The software stops collecting the data automatically after 5 seconds. Apply "Linear Fit" to your velocity data displayed on the graph to get the acceleration of the falling picket fence. Repeat this procedure 5 times.

In GA, create a new manual column. (Hint: Data → New Manual Column "Gravitational Acceleration") Remember to name it and choose an appropriate unit. Then, in GA, enter the values of 5 measured accelerations. Use "Statistics" to find the mean value of the experimental g and the standard deviation. Record this and complete all the questions for Part 3 in the Inlab in WebAssign. Take a screenshot of the statistics graphs with the provided data. Paste and save them in a document in DOC format. Upload this file in the Inlab for Part 3.