2.8 Measuring the Astronomical Unit
Pre-Lecture Reading 2.8
-
•Astronomy Today, 8th Edition (Chaisson & McMillan)
-
•Astronomy Today, 7th Edition (Chaisson & McMillan)
-
•Astronomy Today, 6th Edition (Chaisson & McMillan)
Video Lecture
-
•Measuring the Astronomical Unit (15:12)
Supplementary Notes
Parallax
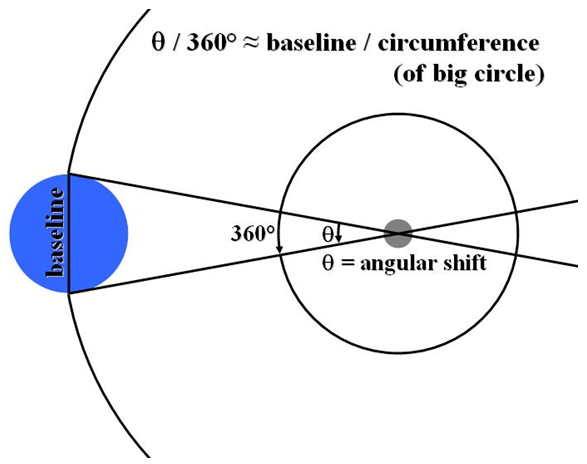
Figure 1: Earth-baseline parallax
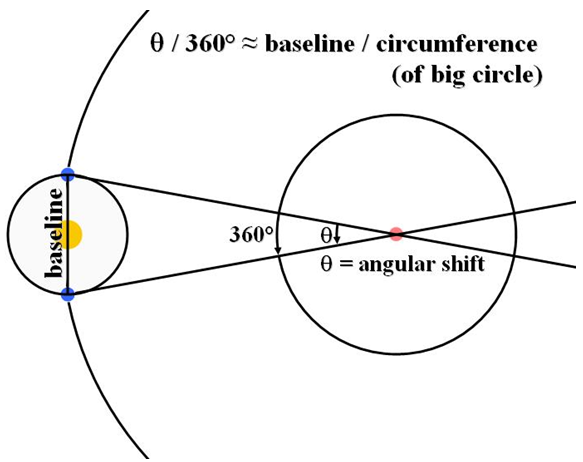
Figure 2: Stellar parallax
-
•In both cases:
-
-
•angular shift = apparent shift in angular position of object when viewed from different observing points
-
•baseline = distance between observing points
-
•distance = distance to object
-
-
•If you know the baseline and the angular shift, solving for the distance yields:
- Note: Angular shift needs to be in degrees when using this equation.
-
•If you know the baseline and the distance, solving for the angular shift yields:
- Note: Baseline and distance need to be in the same units when using this equation.
Standard astronomical baselines
-
•Earth-baseline parallax
-
•baseline = diameter of Earth = 12,756 km
-
•This is used to measure distances to objects within our solar system.
-
-
•Stellar parallax
-
•baseline = diameter of Earth's orbit = 2 astronomical units (or AU)
-
•1 AU is the average distance between Earth and the sun.
-
•This is used to measure distances to nearby stars.
-
Radar Ranging
-
•distance = distance to object
-
•2 × distance = total distance that radio waves travel
-
•c = speed of light = speed of radio waves
-
•time = time that it takes for radio waves to travel to object, reflect, and travel back
Measuring the Astronomical Unit
Step 1
Venus is often the closest planet to Earth, making it a natural target for both Earth-baseline parallax and radar ranging measurements, which yield the distance to Venus in physically meaningful units, such as kilometers.-
•For example, when Venus is at closest approach to Earth, Earth-baseline parallax and radar ranging both measure the distance to Venus to be approximately 4.5 × 107 km.
Step 2
Set the distance to Venus in kilometers equal to the distance to Venus in AU.-
•For example, when Venus is at closest approach to Earth, the distance to Venus is approximately 1 AU – 0.7 AU = 0.3 AU.
-
•Hence: 0.3 AU = 4.5 × 107 km
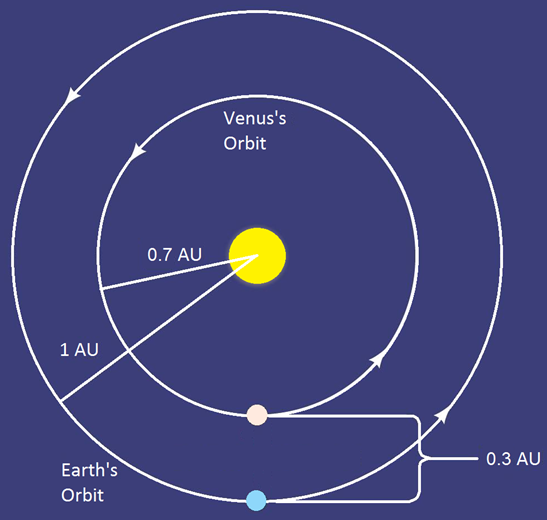
Figure 3
Step 3
Solve for 1 AU.-
•For example, when Venus is at closest approach to Earth:
| 0.3 AU | = | 4.5 × 107 km | ||||
| = |
| ||||
| 1 AU | = | 1.5 × 108 km |
Lab Link
Material presented in this unit is related to material presented in Lab 4 of Astronomy 101 Laboratory: Our Place in Space. In Lab 4: Cosmic Distance Ladder I: Parallax, we:-
•Use parallax to measure distances to objects on Earth.
-
•Use parallax and Earth's diameter to measure distances to objects within our solar system.
-
•Use parallax measurements of objects within our solar system to measure the astronomical unit (AU).
-
•Use parallax and the AU to measure distances to nearby stars.
Video Lab Summary
-
•Cosmic Distance Ladder I: Parallax (29:27)
Assignment 2
-
•Do Questions 7 and 8.


